初中数学一次函数的最值解答题

如图，在平面直角坐标系xOy中，直线AB与x轴交于点A，与y轴交于点B，且OA = 3，AB = 5．点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AO返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB－BO－OP于点E．点P、Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0）．

（1）求直线AB的解析式；
（2）在点P从O向A运动的过程中，求△APQ的面积S与t之间的函数关系式（不必写出t的取值范围）；
（3）在点E从B向O运动的过程中，完成下面问题：
①四边形QBED能否成为直角梯形？若能，请求出t的值；若不能，请说明理由；
②当DE经过点O时，请你直接写出t的值．

（本题6分） 为了促进长三角区域的便捷沟通，实现节时、节能，杭州湾跨海大桥于2008年5月1日通车，下表是宁波到上海两条线路的有关数据：

线路	弯路（宁波—杭州—上海）	直路（宁波—跨海大桥—上海）
路程	316公里	196公里
过路费	140元	180元

（1）若小车的平均速度为80公里/小时，则小车走直路比走弯路节省多少时间？
（2）若小车每公里的油耗为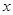升，汽油价格为5.00元/升，问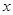为何值时，走哪条线路的总费用较少（总费用=过路费＋油耗费）；

已知平面直角坐标系xOy，一次函数的图像与y轴交于点A，点M在正比例函数的图像上，且MO＝MA．求点M的坐标.

直线y＝x＋2与x轴、y轴分别交于A、B两点，D是x轴上一点，坐标为（x，0），△ABD的面积为S.
（1）求点A和点B的坐标；
（2）求S与x的函数关系式；
（3）当S=12时，求点D的坐标.

本市某旅游度假区每天的赢利额y（元）与售出的门票x（张）之间的函数关系如图所示.

（1）当0≤x≤200，且x为整数时，y关于x的函数解析式为                 ；当200＜x≤300，且x为整数时，y关于x的函数解析式为                .
（2）要使旅游度假区一天的赢利超过1000元，试问
该天至少应售出多少张门票？
（3）请思考并说明图像与y轴交点（0，－1000）的实际意义.

为落实校园“阳光体育”工程，某校计划购买篮球和排球共20个．已知篮球每个80元，排球每个60元．设购买篮球x个，购买篮球和排球的总费用y元．
（1）求y与x之间的函数关系式；
（2）如果要求篮球的个数不少于排球个数的3倍，应如何购买，才能使总费用最少？最少费用是多少元？

小明从地出发向地行走，同时晓阳从地出发向地行走，如图所示，相交于点M的两条线段分别表示小明、晓阳离A地的距离（千米）与已用时间（分钟）之间的关系，

（1）小明与晓阳相遇时，晓阳出发的时间是           ；
（2）求小明与晓阳的速度。

小张骑车往返于甲、乙两地，距甲地的路程（千米）与时间（小时）的函数图象如图所示．

（1）小张在路上停留     小时，他从乙地返回时骑车的速度为     千米／时．
（2）小李与小张同时从甲地出发，按相同路线匀速前往乙地，到乙地停止，途中小李与小张共相遇3次．请在图中画出小李距甲地的路程（千米）与时间（小时）的函数的大致图象．
（3）小王与小张同时出发，按相同路线前往乙地，距甲地的路程（千米）与时间（小时）的函数关系式为．小王与小张在途中共相遇     次？请你计算第一次相遇的时间．

小明和小亮进行赛跑训练，他们选择了一个土坡，按同一路线同时出发，从坡底跑到坡顶再原路返回坡底．他们俩上坡的平均速度不同，下坡的平均速度则是各自上坡平均速度的1.5倍．设两人出发x min后距出发点的距离为y m．图中折线表示小明在整个训练中y与x的函数关系，其中A点在x轴上，M点坐标为(2，0)．

（1）求小明上、下坡的速度及A点的坐标；
（2）小亮上坡平均速度是小明上坡平均速度的一半，那么两人出发后多长时间第一次相遇？

黄冈市英山县有一个茶叶厂，该厂的茶叶主要有两种销售方式，一种方式是卖给茶叶经销商，另一种方式是在各超市的柜台进行销售，每年该厂生产的茶叶都可以全部销售，该茶叶厂每年可以生产茶叶100万盒，其中，卖给茶叶经销商每盒茶叶的利润y₁（元）与销售量x（万盒）之间的函数图如图所示；在各超市柜台销售的每盒利润y₂（元）与销售量x（万盒）之间的函数关系为：

（1）写出该茶叶厂卖给茶叶经销商的销售总利润（万元）与其销售量x（万盒）之间的函数关系式，并指出x的取值范围；
（2）求出该茶叶厂在各超市柜台销售的总利润（万元）与卖给茶叶经销商的销售量x（万盒）之间的函数关系式，并指出x的取值范围；
（3）求该茶叶厂每年的总利润w（万元）与卖给茶叶经销商的销售量x（万盒）之间的函数关系式，并帮助该茶叶厂确定卖给茶叶经销商和在各超市柜台的销量各为多少万盒时，该公司的年利润最大？

顾客李某于今年“五·一”期间到电器商场购买空调，与营业员有如下的一段对话：
顾客李某：A品牌的空调去年“国庆”期间价格为3000元，这次便宜多了，一次就降为2430元，是不是质量有问题？
营业员：不是一次降价，这是第二次降价，今年春节期间已经降了一次价，两次降价的幅度相同．我们所销售的空调质量都是很好的，尤其是A品牌系列空调的质量是一流的．
顾客李某：我们单位的同事也想买一台A品牌的空调，有优惠政策吗？
营业员：有，请看《购买A品牌系列空调的优惠办法》．购买A品牌系列空调的优惠办法：
方案一：各种型号的空调每台价格优惠5%，送货上门，负责安装，每台空调另加运输费和安装费共90元．
方案二：各种型号的空调每台价格优惠2%，送货上门，负责安装，免运输费和安装费．根据以上对话和A品牌系列空调销售的优惠办法，请你回答下列问题：
（1）求A品牌系列空调平均每次降价的百分率？
（2）请你为顾客李某决策，选择哪种优惠更合算，并通过计算说明。                           

某文具店出售书包与文具盒，书包每个定价50元，文具盒每个定价10元．该店制定了两种优惠方案：①买一个书包赠送一个文具盒；②按总价的8.5折(总价的85％)付款．某班学生需购买l2个书包、文具盒若干(不少于12个)。如果设文具盒数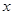个，付款数为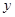元。根据条件解决下列问题：
(1)分别求出两种优惠方案中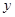与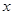之间的关系；
(2)试分析哪一种方案更省钱．

一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售，为了方便，他带了一些零钱备用．他先按市场价售出一些后，又降价出售．售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示，结合图像回答下列问题：

(1)农民自带的零钱是多少?
(2)降价前他每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完，这时他手中的钱(含备用的钱)是450元，问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?

某书报亭开设两种租书方式：一种是零星租书，每册收费1元；另一种是会员卡租书，办卡费每月12元，租书费每册0.4元．小军经常来该店租书，若每月租书数量为x册.
（1）写出零星租书方式应付金额y₁(元)与租书数量x（册）之间的函数关系式；
（2）写出会员卡租书方式应付金额y₂(元 )与租书数量x(册)之间的函数关系式；
（3）小军选取哪种租书方式更合算？

我市某林场计划购买甲、乙两种树苗共800株，甲种树苗每株24元，乙种树苗每株30元．相关资料表明：甲、乙两种树苗的成活率分别为85%，90%．
（1）若购买这两种树苗共用去21000元，则甲、乙两种树苗各购买多少株？
（2）若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？
（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低，并求出最低费用．