[广西]2012届广西桂平市中考模拟训练题(二)数学试卷
据贵港市统计局公布的第六次人口普查数据,本市常住人口411.88万人,其中411.88万人用科学记数法表示为:
A. 人 人 |
B. 人 人 |
C. 人 人 |
D. 人 人 |
单独使用下面形状的五种地地砖:①等边三角形 ②正方形 ③正五边形 ④正六边形 ⑤正八边形.能镶嵌(密铺)地面的是:
| A.③④⑤ | B.①②④ | C.②④⑤ | D.①③④ |
如图所示,AB∥CD,∠E=37°,∠C=20°,则∠EAB的度数为:
| A.57° | B.60° | C.63° | D.123° |
如图,Rt△ 中,∠ACB=90°,
中,∠ACB=90°, ,若把Rt△
,若把Rt△ 绕边
绕边 所在直线旋转一周,则所得几何体的表面积为:
所在直线旋转一周,则所得几何体的表面积为:
A. |
B. |
C. |
D. |

如图,⊙O1 的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,O1O2 =8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现:
| A.3次 | B.5次 | C.6次 | D.7次 |
把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分周长和是:
| A.4n cm | B.4m cm | C.2(m+n) cm | D.4(m-n) cm |

如图,在△ABC中,AB=AC,D、E是△ABC 内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= cm.
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.
其中正确的命题是: .(只要求填写正确命题的序号)
在一个不透明的袋子中装有3个除颜色外完全相同的小球,其中白球1个,黄球1个,红球1个,摸出一个球记下颜色后放回,再摸出一个球,请用列表法或画树状图法求两次都摸到红球的概率.
| |
白 |
黄 |
红 |
| 白 |
白白 |
白黄 |
白红 |
| 黄 |
黄白 |
黄黄 |
黄红 |
| 红 |
红白 |
红黄 |
红红 |
如图, 在平面直角坐标系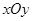 中, 点
中, 点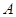 (0,8), 点
(0,8), 点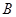 (6 , 8 ).
(6 , 8 ). 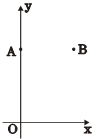
(1)只用直尺(没有刻度)和圆规, 求作一个点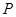 ,使点
,使点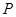 同时满足下列两个条件(要求保留作图痕迹, 不必写出作法):
同时满足下列两个条件(要求保留作图痕迹, 不必写出作法):
①点P到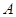 ,
,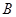 两点的距离相等;
两点的距离相等;
②点P到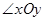 的两边的距离相等.
的两边的距离相等.
(2)在(1)作出点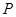 后, 写出点
后, 写出点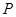 的坐标.
的坐标.
图①表示的是某综合商场今年1~5月的商品各月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题:
(1)来自商场财务部的数据报告表明,商场1~5月的商品销售总额一共是410万元,请你根据这一信息将图①中的统计图补充完整.
(2)商场服装部5月份的销售额是多少万元?
(3)小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了.你同意他的看法吗?请说明理由.
如图,在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥BD交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%,90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.
如图, 为
为 直径,且弦
直径,且弦 于
于 ,过点
,过点 的切线与
的切线与 的延长线交于点
的延长线交于点 .
.
(1)若 是
是 的中点,连接
的中点,连接 并延长
并延长 交
交 于
于 .求证:
.求证: ;
;
(2)若 ,求
,求 的半径.
的半径.





 在数轴上表示正确的是:
在数轴上表示正确的是:
 关于原点中心对称的点是:
关于原点中心对称的点是:



 ,滑梯的坡角为
,滑梯的坡角为 ,那么滑梯长
,那么滑梯长 为:
为:




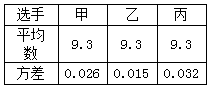
 = .
= .
 ,则
,则 .
.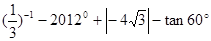


 粤公网安备 44130202000953号
粤公网安备 44130202000953号