已知y-3与4x-2成正比例,且当x=1时,y=5.
(1)求y与x函数关系式;
(2)求当x=-2时的函数值.
已知:如图1,一次函数y=mx+5m的图象与x轴、y轴分别交于点A、B,与函数y=- x的图象交于点C,点C的横坐标为-3.
x的图象交于点C,点C的横坐标为-3.
(1)求点B的坐标;
(2)若点Q为直线OC上一点,且S△QAC=3S△AOC,求点Q的坐标;
(3)如图2,点D为线段OA上一点,∠ACD=∠AOC.点P为x轴负半轴上一点,且点P到直线CD和直线CO的距离相等.
①在图2中,只利用圆规作图找到点P的位置;(保留作图痕迹,不得在图2中作无关元素.)
②求点P的坐标.
自2012年6月1日起,全国实施了阶梯电价.某省出台了阶梯电价方案:电价分“三档”收费,第一档为a度,居民用电量低于a度的部分,执行现行的标准电价(0.53元/度);第二档为a~b度,居民月用电量在a~b之间的部分,电价在一档电价的基础上提高0.05元/度;第三档为超过b度,居民月用电量高于b度的部分,电价在一档电价的基础上提高m元/度.实施阶梯电价后,月电费y(元)与月用电量x(度)之间的函数关系如图所示.
(1)求a,b,m的值;
(2)求y与x之间函数关系式,并写出自变量x的取值范围.
已知一次函数y=kx+b的图象经过点(-2,4),且与正比例函数y=2x的图象平行.
(1)求一次函数y=kx+b的解析式;
(2)求一次函数y=kx+b的图象与坐标轴所围成的三角形的面积;
(3)若A(a,y1),B(a+b,y2)为一次函数y=kx+b的图象上两个点,试比较y1与y2的大小.
已知一次函数y=2x-3.
(1)当x=-2时,求y.
(2)当y=1时,求x.
(3)当-3<y<0时,求x的取值范围.
某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(千克)的一次函数,现已知李明带了60千克的行李费,交了行李费5元;张华带了90千克的行李,交了行李费10元.
(1)写出y与x之间的函数表达式.
(2)旅客最多可免费携带多少千克的行李?
一水池的容积是90m3,现蓄水10m3,用水管以5m3/h的速度向水池中注水.
(1)写出水池蓄水量V(m3)与进水时间t(h)之间的函数解析式;
(2)当t=10h,V的值是多少?
如图,在平面直角坐标系中,直线 分别交x轴、y轴于A、B两点.
分别交x轴、y轴于A、B两点.
(1)求A、B两点的坐标;
(2)设P是直线AB上一动点(点P与点A不重合),⊙P始终和x轴相切,和直线AB相交于C、D两点(点C的横坐标小于点D的横坐标).若P点的横坐标为m,试用含有m的代数式表示点C的横坐标;
(3)在(2)的条件下,若点C在线段AB上,当△BOC为等腰三角形时求m的值.
在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.
实验操作
在平面直角坐标系中描出点P从点O出发,平移1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中.
观察思考
任一次平移,点P可能到达的点在我们学过的一次函数的图像上,如:平移1次后点P在函数_______________的图像上;平移2次后点P在函数_________________的图像上
规律发现:由此我们知道,平移n次后点P在函数__________________的图像上(请填写相应的解析式)
在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:

(1)甲、乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽甲所用的时间为 .
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么时间段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡低?
某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,工厂需要一次性投入机器租赁、安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱 个,请分别写出从纸箱厂购买纸箱的费用y(元)和蔬菜
个,请分别写出从纸箱厂购买纸箱的费用y(元)和蔬菜加工厂自己加工制作纸箱的费用y2(元)关于 (个)的函数关系式;
(个)的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作:


请根据图中给出的信息,解答下列问题:
(1)放入一个小球量筒中水面升高_______cm;
(2)求放入小球后量筒中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);
(3)量筒中至少放入几个小球时有水溢出?
已知:y-1与x+2成正比例,且x=1时,y=4.
(1)写出 与
与 之间的函数关系式;
之间的函数关系式;
(2)在图中画出此函数的图像;
(3) 求此直线与坐标轴围成的三角形的面积.
(4)观察图像,直接写出 时
时 的取值范围.
的取值范围.
如图,一次函数 的图像与反比例函数
的图像与反比例函数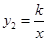 (
(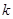 为常数,且
为常数,且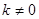 )的图像都经过点
)的图像都经过点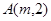
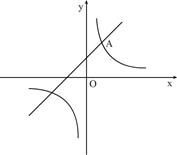
(1)求点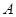 的坐标及反比例函数的表达式;
的坐标及反比例函数的表达式;
(2)结合图像直接比较:当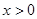 时,
时,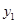 和
和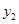 的大小.
的大小.