初中数学一次函数的最值解答题

如图，已知点A（a，3）是一次函数y₁=x+b图象与反比例函数y₂=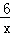图象的一个交点．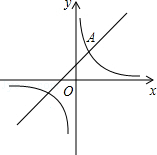

（1）求一次函数的解析式；
（2）在y轴的右侧，当y₁＞y₂时，直接写出x的取值范围．

已知直线y＝－2x＋4与x轴交于A点，与y轴交于B点．
(1)求A、B两点的坐标；
(2)求直线y＝－2x＋4与坐标轴围成的三角形的面积．

在平面直角坐标系中，点A，B的坐标分别为（4，0），（0，4），直线y=x+b和线段AB交于点D，DE⊥x轴，垂足为点E，DF⊥y轴，垂足为点F，记w=DF﹣DE，当1≤w≤2时，求b的取值范围．

函数常用的表示方法有三种．
已知A、B两地相距30千米，小王以40千米/时的速度骑摩托车从A地出发匀速前往B地参加活动．请选择两种方法来表示小王与B地的距离y（千米）与行驶时间x（小时）之间的函数关系．

如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，-2）．

（1）求直线AB的解析式；
（2）直线AB上是否存在点C，使△BOC的面积为2？若存在，求出点C的坐标；若不存在，请说明理由．

已知一次函数，
（1）为何值时，它的图象经过原点；
（2）为何值时，它的图象经过点（0，）.

如图，在平面直角坐标系内，梯形OABC的顶点坐标分别是：A（3，4），B（8，4），C（11，0），点P（t，0）是线段OC上一点，设四边形ABCP的面积为S．

（1）过点B作BE⊥x轴于点E，则BE=         ，用含t的代数式表示PC=           ．
（2）求S与t的函数关系．
（3）当S＝20时，直接写出线段AB与CP的长．

已知一次函数的图象经过点（3，6）与点（，﹣），求这个函数的解析式．

如图，一次函数y＝x＋6与反比例函数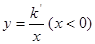的图象相交于A，B两点，与x轴、y轴交于E、F，点B的横坐标为。

（1）试确定反比例函数的解析式；
（2）求点E、F的坐标。

已知一次函数y=kx+b．当x=1时，y=1；当x=2时，y=﹣1．求这个函数的表达式．

如图，函数的图象与函数（）的图象交于A（，1）B（1，）两点．

（1）求函数的表达式；    
（2）观察图象，比较当时，与的大小．

如图，直线l：y=x+6交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．

（1）点A坐标是      ，点B的坐标      ，BC=      ．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．

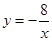如图，已知一次函数的图象与反比例函数的图象交于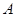，两点，且点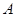的横坐标和点的纵坐标都是．

求：（1）一次函数解析式；
（2）求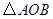的面积．

开学初，小明到文具批发部一次性购买某种笔记本，该文具批发部规定：这种笔记本售价y（元/本）与购买数量x（本）之间的函数关系如图所示．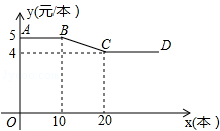

（1）图中线段AB所表示的实际意义是     ；
（2）请直接写出y与x之间的函数关系式；
（3）已知该文具批发部这种笔记本的进价是3元/本，若小明购买此种笔记本超过10本但不超过20本，那么小明购买多少本时，该文具批发部在这次买卖中所获的利润W（元）最大？最大利润是多少？

（本小题12分）如图，直线分别交轴于、，点是该直线与反比例函数在第一象限内的一个交点，轴于，且.

（1）求点的坐标；
（2）设点与点在同一个反比例函数的图象上，且点在直线的右侧，作轴于，当与相似时，求点的坐标.