画出函数y=﹣x+1的图象,结合图象,回答下列问题.
在函数y=﹣x+1的图象中:
(1)画出函数图象并写出与x轴的交点坐标是 _________ ;
(2)随着x的增大,y将 _________ (填“增大”或“减小”);
(3)当y取何值时,x<0? _________
(4)把它的图象向下平移2个单位长度则得到的新的一次函数解析式是 _________ .
年春季,我国云南、贵州等西南地区遇到多年不遇旱灾,“一方有难,八方支援”,为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水灌溉农及田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时,灌溉农田32亩.
(1)设甲种柴油发电机数量为x台,乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量;
②求出y与x的函数关系式;
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元,应如何安排三种柴油发电机的数量,既能按要求抽水灌溉,同时柴油发电机总费用W最少?
(本题8分)阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线L1,一次函数y=k2x+b2(k2≠0)的图象为直线L2,若k1=k2,且b1≠b2,我们就称直线L1与直线L2互相平行.解答下面的问题:
(1)求过点P(1,4),且与直线y=-2x-1平行的直线L的函数解析式,并画出直线L的图象;
(2)设直线L分别与y轴,x轴交于点A,B,如果直线m:y=kx+t(t>0)与直线L平行,且交x轴于点C,求出△ABC的面积S关于t函数解析式.
某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
、(8分)已知一次函数y=Kx+b的图象过点(3,5)与(-4,-9),(1)求这个一次函数解析式。
(2)利用函数图象求当x为何值时,y>0。
如图,已知一次函数y=kx+b的图象经过点(0,4)和(1,6),
(1)求这个函数表达式并判断(-3,-2)是否在此函数的图象上;
(2)求该函数图像与x轴、y轴围成三角形的面积。
如图,直线l:y= x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.
x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.

(1)点A坐标是 ,点B的坐标 ,BC= .
(2)当点P在什么位置时,△APQ≌△CBP,说明理由.
(3)当△PQB为等腰三角形时,求点P的坐标.
如图,已知一次函数 的图象与反比例函数
的图象与反比例函数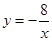 的图象交于
的图象交于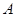 ,
, 两点,且点
两点,且点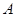 的横坐标和
的横坐标和 点的纵坐标都是
点的纵坐标都是 .
.
求:(1)一次函数解析式;
(2)求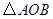 的面积.
的面积.
开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.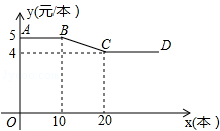
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
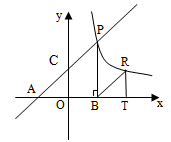
(本小题12分)如图,直线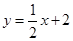 分别交轴于
分别交轴于 、
、 ,点
,点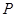 是该直线与反比例函数在第一象限内的一个交点,
是该直线与反比例函数在第一象限内的一个交点,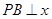 轴于
轴于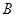 ,且
,且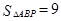 .
.
(1)求点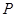 的坐标;
的坐标;
(2)设点 与点
与点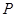 在同一个反比例函数的图象上,且点
在同一个反比例函数的图象上,且点 在直线
在直线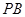 的右侧,作
的右侧,作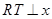 轴于
轴于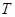 ,当
,当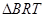 与
与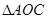 相似时,求点
相似时,求点 的坐标.
的坐标.
如图,反比例函数 与一次函数y=x+b的图象,都经过点A(1,2)
与一次函数y=x+b的图象,都经过点A(1,2)
(1)试确定反比例函数和一次函数的解析式;
(2)求一次函数图象与两坐标轴的交点坐标.