湖南省邵阳市八年级下学期期末考试数学试卷
下列四组线段中,可以构成直角三角形的是( )
| A.1,2,3 | B.2,3,4 | C.3,4,5 | D.4,5,6 |
在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,且满足∠A:∠B:∠C=1:2:3,则△ABC一定是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
在平面直角坐标系中,点P(﹣3,4)关于x轴的对称点的坐标是( )
| A.(﹣4,﹣3) | B.(﹣3,﹣4) | C.(3, 4) | D.(3,﹣4) |
下列函数:①y=x;②y= ;③y=
;③y= ;④y=2x+1,其中一次函数的个数是( )
;④y=2x+1,其中一次函数的个数是( )
| A.1 | B.2 | C.3 | D.4 |
要了解八年级学生身高在某一范围内学生所占比例,需知道相应的( )
| A.平均数 | B.众数 | C.中位数 | D.频数 |
菱形的两条对角线长分别为6cm、8cm,则它的面积为( )cm2.
| A.6 | B.12 | C.24 | D.48 |
已知一次函数y=kx+b(k≠0)的草图如图所示,则下列结论正确的是( )
| A.k>0,b>0 | B.k>0,b<0 | C.k<0,b>0 | D.k<0,b<0 |
如图,如果张力的位置可表示为(1,3),则王红的位置应表示为( )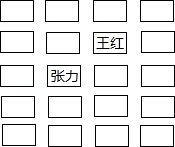
| A.(4,1) | B.(4,2) | C.(2,4) | D.(3,4) |
顺次连结四边形ABCD各边中点得到的四边形一定是( )
| A.矩形 | B.正方形 | C.平行四边形 | D.菱形 |
甲、乙两人赛跑,所跑路程与时间的关系如图(实线为甲的路程与时间的关系图象,虚线为乙的路程与时间的关系图象),小王根据图象得到如下四条信息,其中错误的是( )
| A.这是一次1500m赛跑 |
| B.甲、乙同时起跑 |
| C.甲、乙两人中先到达终点的是乙 |
| D.甲在这次赛跑中的速度为5m/s |
在女子3000米的长跑中,运动员的平均速度v= ,则这个关系式中自变量是 _________ .
,则这个关系式中自变量是 _________ .
把40个数据分在4个组内,第一、二、四组中的数据分别为7,6,15,则第三组的频数为 _________ ,频率为 _________ .
如图,已知一次函数y=ax+b和正比例函数y=kx的图象交于点A,则根据图象可得,关于x,y的二元一次方程组 的解是 _________ .
的解是 _________ .
如图,梯形ABCD中,AB∥DC,DE∥CB,△AED的周长为16,EB=3,则梯形ABCD的周长为 _________ .
如图,在平面直角坐标系中,已知A(﹣1,5),B(﹣1,0),C(﹣4,3).
①在图中作出△ABC关于y轴的对称图形△A1B1C1;
②写出点A1和C1的坐标.
如图,在▱ABCD中,AE⊥BC,AF⊥DC,垂足分别为E、F,∠ADC=60°,BE=4,CF=2.
(1)从对称性质看,▱ABCD是 _________ 对称图形;
(2)求平行四边形ABCD的周长.
某学校为丰富课间自由活动的内容,随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么”,整理收集到的数据,绘制成直方图,如图.
(1)喜欢“踢毽子”的学生有 _________ 人,并在图中将“踢毽子”部分的条形图补充完整;
(2)喜欢“跳绳”的频率是 _________ ;
(3)该校共有800名学生,估计喜欢“跳绳”的学生有 _________ 人.
画出函数y=﹣x+1的图象,结合图象,回答下列问题.
在函数y=﹣x+1的图象中:
(1)画出函数图象并写出与x轴的交点坐标是 _________ ;
(2)随着x的增大,y将 _________ (填“增大”或“减小”);
(3)当y取何值时,x<0? _________
(4)把它的图象向下平移2个单位长度则得到的新的一次函数解析式是 _________ .
如图,在△ABC中;
(1)作∠C的角平分线CE交AB于E(保留痕迹,不写作法),过点E分别作AC、BC的垂线EM、EN,垂足分别为M、N;
(2)若EN=2,AC=4,求△ACE的面积.
在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A、B的横坐标分别为a+2与2a﹣5,且关于y轴对称,BC的长为3,且点C在第三象限.
(1)求顶点A、C的坐标;
(2)若y=kx+b是经过点B,且与AC平行的一条直线,试确定它的解析式.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号