甲骑车到乙家研讨数学问题,中途因等候红灯停止了一分钟,之后又骑行了1.2千米到达了乙家.若甲骑行的速度始终不变,从出发开始计时,剩余的路程 (单位:千米)与时间
(单位:千米)与时间 (单位:分钟)的函数关系的图象如图所示,则图中a等于
(单位:分钟)的函数关系的图象如图所示,则图中a等于
| A.1.2 | B.2 | C.2.4 | D.6 |
正方形ABCD中,点P从点C出发沿着正方形的边依次经过点D,A向终点B运动,运动的路程为x(cm),△PBC的面积为y( ),y随x变化的图象可能是( )
),y随x变化的图象可能是( )

大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系。下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是

如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则B’点的坐标为
A.(2,2 ) ) |
B.( ,2- ,2- ) ) |
C.(2,4-2 ) ) |
D.( ,4-2 ,4-2 ) ) |
如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是

| A.18 | B.16 | C.10 | D.20 |
图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
| A.体育场离张强家2.5千米 |
| B.张强在体育场锻炼了15分钟 |
| C.体育场离早餐店4千米 |
| D.张强从早餐店回家的平均速度是3千米/小时 |
李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是( )
A. |
B. |
C. |
D. |
如图,某电信公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(元)
之间的关系,则下列结论中正确的有
(1)若通话时间少于120分,则A方案比B方案便宜20元
(2)若通话时间超过200分,则B方案比A方案便宜12元
(3)若通讯费用为60元,则B方案比A方案的通话时间多
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分
A.1个 B.2个 C.3个 D.4个
用图象法解某二元一次方程组时,如图所示在同一直角坐标系中作出相应的两个一次函数的图象,则所解的二元一次方程组是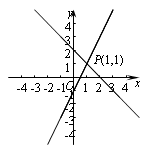
A.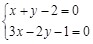 |
B.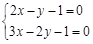 |
C.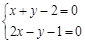 |
D.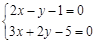 |
如图,点A的坐标为(-1,0),点B在直线 上运动,当线段AB最短时,点B的坐标是( )
上运动,当线段AB最短时,点B的坐标是( )
A.( , , ) ) |
B.( , , ) ) |
C.(- , , ) ) |
D.( , , ) ) |