初中数学一次函数的最值试题

学校需要到印刷厂印刷x份材料，甲印刷厂提出：每份材料收0.2元印刷费，另收500元制版费；乙印刷厂提出：每份材料收0.4元印刷费，不收制版费．
（1）两印刷厂的收费各是多少元？（用含x的代数式表示）
（2）学校要印刷2400份材料，若不考虑其他因素，选择哪家印刷厂比较合算？试说明理由．

煤炭是攀枝花的主要矿产资源之一，煤炭生产企业需要对煤炭运送到用煤单位所产生的费用进行核算并纳入企业生产计划．某煤矿现有1000吨煤炭要全部运往A．B两厂，通过了解获得A．B两厂的有关信息如下表（表中运费栏“元/t•km”表示：每吨煤炭运送一千米所需的费用）：

厂别	运费（元/t•km）	路程（km）	需求量（t）
A	0.45	200	不超过600
B	a（a为常数）	150	不超过800

（2）请你运用函数有关知识，为该煤矿设计总运费最少的运送方案，并求出最少的总运费（可用含a的代数式表示）

（本题12分）如图1，已知在直角坐标系XOY中，正△OBC的边长和等腰直角△DEF的底边都为6，点E与坐标原点O重合，点D、B在X轴上，连结FC，在△DEF沿X轴的正方向以每秒个单位运动时，边EF所在直线和边OC所在直线相交于G，设运动时间为t.

（1）如图2，当t=1时，①求OE的长；②求∠FGC的度数；③求G点坐标；
（2）①如图3，当t为多少时，点F恰在△OBC的OC边上；
②在点F、C、G三点不共线时，记△FCG的面积为S，用含t的代数式表示S，并写出t的相应取值范围.

为了发展旅游经济，我市某风景区对门票采用灵活的售票方法吸引游客，门票的定价为每人50元，，非节日打a折售票，节假日按团队人数分段定价售票，即m人一下（含m人）的团队按原价售票；超过m人的团队，其中m人仍按原价售票，超过m人的部分的游客打b折售票，设某旅游团人数为x人，非节假日购票款为y（元），节假日购票款为y（元）。y 、y与x之间的函数图像如图所示

（1）观察图像可知a=  ，b=   ，m=   
（2）直接写出y， y与x之间的函数解析式
（3）某旅行社导游王娜于5月1日带A团，5月20日（非节假日）带B团到该景区旅游，共付门票款1900元，A、B两个团队合计50人，求A、B两个团队各有多少人？

甲、乙两人在100米直道AB上练习匀速往返跑，若甲、乙分别在A，B两端同时出发，分别到另一端点掉头，掉头时间不计，速度分别为5m/s和4m/s．
（1）在坐标系中，虚线表示乙离A端的距离s（单位：m）与运动时间t（单位：s）之间的函数图象（0≤t≤200），请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象（0≤t≤200）；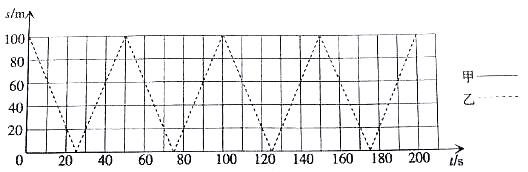

（2）根据（1）中所画图象，完成下列表格：

两人相遇次数 （单位：次）	1	2	3	4	…	n
两人所跑路程之和（单位：m）	100	300			…

 
（3）①直接写出甲、乙两人分别在第一个100m内，s与t的函数解析式，并指出自变量t的取值范围；
②求甲、乙第6此相遇时t的值．

如图1，在平面直角坐标系中，矩形OABC的顶点O在坐标原点，顶点A、C分别在x轴、y轴的正半轴上，且OA＝2，OC＝1，矩形对角线AC、OB相交于E，过点E的直线与边OA、BC分别相交于点G、H．
(1)①直接写出点E的坐标：　　．
②求证：AG＝CH．
(2)如图2，以O为圆心，OC为半径的圆弧交OA与D，若直线GH与弧CD所在的圆相切于矩形内一点F，求直线GH的函数关系式．
(3)在(2)的结论下，梯形ABHG的内部有一点P，当⊙P与HG、GA、AB都相切时，求⊙P的半径．

如图，已知直线AB分别交x轴、y轴于点A（﹣4，0）、B（0，3），点P从点A出发，以每秒1个单位的速度沿直线AB向点B移动，同时，将直线以每秒0．6个单位的速度向上平移，分别交AO、BO于点C、D，设运动时间为t秒（0＜t＜5）．
（1）证明：在运动过程中，四边形ACDP总是平行四边形；
（2）当t取何值时，四边形ACDP为菱形？且指出此时以点D为圆心，以DO长为半径的圆与直线AB的位置关系，并说明理由．

如图，直线y=kx+c与抛物线y=ax²+bx+c的图象都经过y轴上的D点，抛物线与x轴交于A、B两点，其对称轴为直线x=1，且OA=OD．直线y=kx+c与x轴交于点C（点C在点B的右侧）．则下列命题中正确命题的个数是（ ）
①abc＞0；②3a+b＞0；③﹣1＜k＜0；④k＞a+b；⑤ac+k＞0．

A．1    B．2    C．3    D．4

某厂每月固定生产甲、乙两种礼品共100万件，甲礼品每件成本15元，乙礼品每件成本12元，现甲礼品每件售价22元，乙礼品每件售价18元，且都能全部售出．
（1）若某月甲礼品的产量为x万件，总利润为y万元，写出y关于x的函数关系式．
（2）如果每月投入的总成本不超过1380万元，应怎样安排甲、乙礼品的产量，可使所获得的利润最大？

如图，点A是反比例函数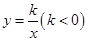 图像上的一点，过点A作AB⊥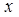轴于点B，且△AOB的面积为2，点A的坐标为．

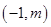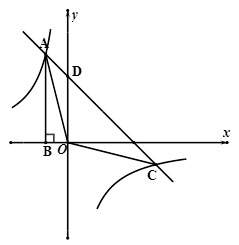
（1）求m和k的值． 
（2）若一次函数y=ax+3的图像经过点A，交双曲线的另一支于点C，交y轴于点D，求△AOC的面积．
（3）在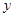轴上是否存在点P，使得△PAC的面积为6？如果存在，请求出点P的坐标；若不存在，请说明理由．

画出一次函数的图像，并求函数图像与两坐标轴所围成的三角形面积．

如图1所示，某乘客乘高速列车从甲地经过乙地到丙地，列车匀速行驶，图2为列车离乙地路程y（千米）与行驶时间x（小时）时间的函数关系图象． 
（1）填空：甲、丙两地距离         千米． 
（2）求高速列车离乙地的路程y与行驶时间x之间的函数关系式，并写出x的取值范围．

如图，二次函数与x轴交于A、B两点，与y轴交于C点，点P从A点出发，以1个单位每秒的速度向点B运动，点Q同时从C点出发，以相同的速度向y轴正方向运动，运动时间为t秒，点P到达B点时，点Q同时停止运动，设PQ交直线AC于点G，

（1）求直线AC的解析式；
（2）设△PQC的面积为S，求S关于t的函数解析式；
（3）在y轴上找一点M，使△MAC和△MBC都是等腰三角形，直接写出所有满足条件的M点的坐标；
（4）过点P作PE⊥AC，垂足为E，当P点运动时，线段EG的长度是否发生改变，请说明理由，

小芳步行上学，最初以某一速度匀速前进，中途遇红灯，稍作停留后加快速度跑步去上学，到校后，她请同学们画出她行进路程s（米）与行进时间t（分钟）的函数图象的示意图.你认为正确的是（   ）

已知：如图，点B在y轴的负半轴上，点A在x轴的正半轴上，且OA=2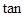，∠OAB=2。

（1）求点B的坐标；
（2）求直线AB的解析式；
（3）若点C的坐标为（-2,0），在直线AB上是否存在一点P，使ΔAPC与ΔAOB相似，若存在，求出点P的坐标；若不存在，请说明理由。