初中数学一次函数的最值试题

若点（-4，y₁），（2，y₂）都在直线y=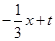上，则y₁与y₂的大小关系是（ ）

A．y1＞y2

B．y1=y2

C．y1＜y2

D．无法确定

已知：如图1，一次函数y=mx+5m的图象与x轴、y轴分别交于点A、B，与函数y=-x的图象交于点C，点C的横坐标为-3．
（1）求点B的坐标；
（2）若点Q为直线OC上一点，且S_△QAC=3S_△AOC，求点Q的坐标；
（3）如图2，点D为线段OA上一点，∠ACD=∠AOC．点P为x轴负半轴上一点，且点P到直线CD和直线CO的距离相等．
①在图2中，只利用圆规作图找到点P的位置；（保留作图痕迹，不得在图2中作无关元素．）
②求点P的坐标．

自2012年6月1日起，全国实施了阶梯电价．某省出台了阶梯电价方案：电价分“三档”收费，第一档为a度，居民用电量低于a度的部分，执行现行的标准电价（0．53元/度）；第二档为a～b度，居民月用电量在a～b之间的部分，电价在一档电价的基础上提高0．05元/度；第三档为超过b度，居民月用电量高于b度的部分，电价在一档电价的基础上提高m元/度．实施阶梯电价后，月电费y（元）与月用电量x（度）之间的函数关系如图所示．

（1）求a，b，m的值；
（2）求y与x之间函数关系式，并写出自变量x的取值范围．

已知一次函数y=kx+b的图象经过点（-2，4），且与正比例函数y=2x的图象平行．
（1）求一次函数y=kx+b的解析式；
（2）求一次函数y=kx+b的图象与坐标轴所围成的三角形的面积；
（3）若A（a，y₁），B（a+b，y₂）为一次函数y=kx+b的图象上两个点，试比较y₁与y₂的大小．

已知一次函数y=2x-3．
（1）当x=-2时，求y．
（2）当y=1时，求x．
（3）当-3＜y＜0时，求x的取值范围．

如图，点Q在直线y=-x上运动，点A的坐标为（1，0），当线段AQ最短时，点Q的坐标为           ．

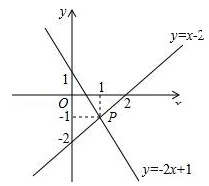
如图，已知函数y=x-2和y=-2x+1的图象交于点P，根据图象可得方程组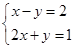的解是                 ．

把函数y=3x的图象沿x轴向左平移1个单位长度，得到的函数表达式是         ．

若一次函数的图象过点（0，2），且函数y随自变量x的增大而增大，请写出一个符合要求的一次函数表达式：             ．

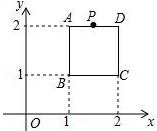
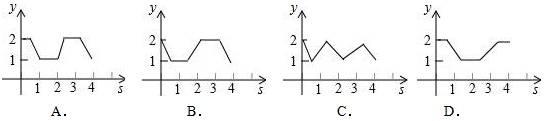
如图，在平面直角坐标系中，边长为1的正方形ABCD中，AD边的中点处有一动点P，动点P沿P→D→C→B→A→P运动一周，则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是（ ）

已知正比例函数y=kx（k≠0）的函数值y随x的增大而减小，则一次函数y=kx+k的图象经过的象限为（ ）

A．二、三、四	B．一、二、四
C．一、三、四	D．一、二、三

某长途汽车客运站规定，乘客可以免费携带一定质量的行李，但超过该质量则需购买行李票，且行李费y（元）是行李质量x（千克）的一次函数，现已知李明带了60千克的行李费，交了行李费5元；张华带了90千克的行李，交了行李费10元．
（1）写出y与x之间的函数表达式．
（2）旅客最多可免费携带多少千克的行李？

一水池的容积是90m³，现蓄水10m³，用水管以5m³/h的速度向水池中注水．
（1）写出水池蓄水量V（m³）与进水时间t（h）之间的函数解析式；
（2）当t=10h，V的值是多少？

若一次函数y=kx+2的图象经过点（2，10），则k的值为                 ．

如图，已知函数y=x-2和y=-2x+1的图象交于点P，根据图象可得方程组的解是           ．