如图,在平面直角坐标系中,顶点为(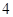 ,
,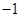 )的抛物线交
)的抛物线交 轴于
轴于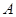 点,交
点,交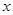 轴于
轴于 ,
,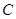 两点(点
两点(点 在点
在点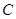 的左侧).已知
的左侧).已知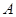 点坐标为(
点坐标为( ,
, ).
).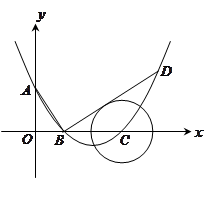
(1)求此抛物线的解析式;
(2)过点 作线段
作线段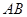 的垂线交抛物线于点
的垂线交抛物线于点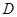 , 如果以点
, 如果以点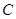 为圆心的圆与直线
为圆心的圆与直线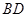 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴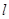 与⊙
与⊙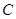 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于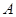 ,
,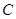 两点之间,问:当点
两点之间,问:当点 运动到什么位置时,
运动到什么位置时,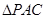 的面积最大?并求出此时
的面积最大?并求出此时 点的坐标和
点的坐标和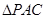 的最大面积.
的最大面积.
如图1:矩形OABC的顶点A、B在抛物线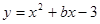 上,OC在
上,OC在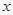 轴上,且
轴上,且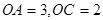 .
.
(1)求抛物线的解析式及抛物线的对称轴.
(2)如图2,边长为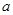 的正方形ABCD的边CD在
的正方形ABCD的边CD在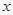 轴上,A、B两点在抛物线上,请用含
轴上,A、B两点在抛物线上,请用含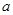 的代数式表示点B的坐标,并求出正方形边长
的代数式表示点B的坐标,并求出正方形边长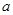 的值.
的值.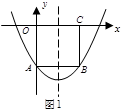
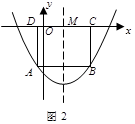
我市某工艺品厂生产一款工艺品.已知这款工艺品的生产成本为每件60元.经市场调研发现:该款工艺品每天的销售量y件与售价x元之间存在着如下表所示的一次函数关系.
| 售价x元 |
… |
70 |
90 |
… |
| 销售量y件 |
… |
3000 |
1000 |
… |
(1)求销售量y件与售价x元之间的函数关系式;
(2)设每天获得的利润为 元,当售价x为多少时,每天获得的利润最大?并求出最大值.
元,当售价x为多少时,每天获得的利润最大?并求出最大值.
如图所示,在平面直角坐标中,抛物线的顶点P到x轴的距离是4,抛物线与x轴相交于O、M两点,OM=4;矩形ABCD的边BC在线段的OM上,点A、D在抛物线上.
(1)求这条抛物线的解析式;
(2)设D(m,n),矩形ABCD的周长为l,写出l与m的关系式,并求出l的最大值;
(3)点E在抛物线的对称轴上,在抛物线上是否还存在点F,使得以E、F、O、M为顶点的四边形是平行四边形?如果存在,写出F点的坐标.
已知二次函数y=2(x﹣3)2+1,下列说法:
①其图象的开口向下;
②其图象的对称轴为直线x=﹣3;
③其图象顶点坐标为(3,﹣1);
④当x<3时,y随x的增大而减小.
则其中说法正确的有
| A.1个 | B.2个 | C.3个 | D.4个 |
抛物线 的部分图象如图所示,交x轴于(1,0),对称轴是直线x = —1,
的部分图象如图所示,交x轴于(1,0),对称轴是直线x = —1,
若y>0,则x的取值范围是( )

| A.-4< x <1 | B.-3< x <1 |
| C.x <-4或x >1 | D.x <-3或x >1 |