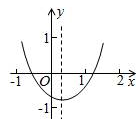
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中所有正确结论的序号是 .
如果函数y=(k-3)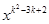 +kx+1是二次函数,那么k的值一定是 .
+kx+1是二次函数,那么k的值一定是 .
若二次函数y=ax2+bx+a2-2(a,b为常数)的图象如下,则a的值为( )
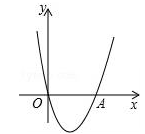
| A.-2 | B.-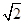 |
C.1 | D.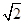 |
如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点,抛物线的顶点为D.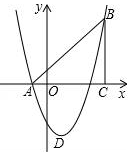
(1)求b,c的值;
(2)点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下:
①求以点E、B、F、D为顶点的四边形的面积;
②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,说明理由.
某商场购进一批L型服装(数量足够多),进价为40元/件,以60元/件销售,每天销售20件,根据市场调研,若每件降价1元,则每天销售数量比原来多3件.现商场决定对L型服装开展降价促销活动,每件降价x元(x为正整数).在促销期间,商场要想每天获得最大销售毛利润,每件应降价多少元?每天最大销售毛利润为多少?(注:每件服装销售毛利润是指每件服装的销售价与进货价的差)
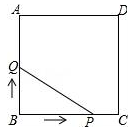
如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:
(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )

| A.2个 | B.3个 | C.4个 | D.1个 |
将二次函数y=x2的图象向右平移一个单位长度,再向上平移3个单位长度所得的图象解析式为( )
| A.y=(x-1)2+3 | B.y=(x+1)2+3 |
| C.y=(x-1)2-3 | D.y=(x+1)2-3 |
如图,在平面直角坐标系中,直线 与抛物线
与抛物线 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为 ,点P的横坐标为
,点P的横坐标为 ,求
,求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 的最大值;
的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在 轴上时,求出对应点P的坐标.
轴上时,求出对应点P的坐标.
某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润 (元)与销售单价
(元)与销售单价 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
如图二次函数 的图象经过A(-1,0)和B(3,0)两点,且交
的图象经过A(-1,0)和B(3,0)两点,且交 轴于点C.
轴于点C.
(1)试确定 、
、 的值;
的值;
(2)若点M为此抛物线的顶点,求△MBC的面积.
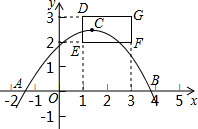
如图,抛物线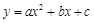 与
与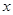 轴的一个交点A在点(-2,0)和(1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则
轴的一个交点A在点(-2,0)和(1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则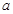 的取值范围是 .
的取值范围是 .
已知抛物线 (
( <0)过A(
<0)过A( ,0)、O(0,0)、B(
,0)、O(0,0)、B( ,
, )、C(3,
)、C(3, )四点.则
)四点.则
 (用“<”,“>”或“=”填空).
(用“<”,“>”或“=”填空).
二次函数 (a,b,c为常数,且
(a,b,c为常数,且 )中的
)中的 与
与 的部分对应值如表:
的部分对应值如表:
 |
… |
-1 |
0 |
1 |
3 |
… |
 |
… |
-1 |
3 |
5 |
3 |
… |
下列结论:
(1) ;
;
(2)当 时,y的值随x值的增大而减小;
时,y的值随x值的增大而减小;
(3)3是方程 的一个根;
的一个根;
(4)当 时,
时, .
.
其中正确的个数为 ( )
A.4个 B.3个 C.2个 D.1个