如图,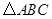 为直角三角形,
为直角三角形,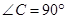 ,
,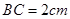 ,
,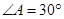 ;四边形
;四边形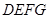 为矩形,
为矩形,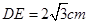 ,
,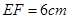 ,且点
,且点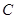 、
、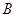 、
、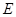 、
、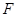 在同一条直线上,点
在同一条直线上,点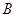 与点
与点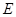 重合.
重合.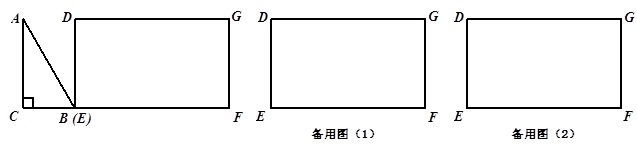
(1)求边
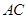 的长;
的长;(2)将
 以每秒
以每秒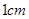 的速度沿矩形
的速度沿矩形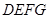 的边
的边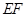 向右平移,当点
向右平移,当点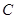 与点
与点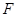 重合时停止移动,设
重合时停止移动,设 与矩形
与矩形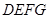 重叠部分的面积为
重叠部分的面积为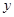 ,请求出重叠部分的面积
,请求出重叠部分的面积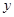 (
(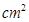 )与移动时间
)与移动时间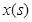 的函数关系式(时间不包含起始与终止时刻);
的函数关系式(时间不包含起始与终止时刻);(3)在(2)的基础上,当
 移动至重叠部分的面积为
移动至重叠部分的面积为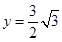
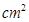 时,将
时,将 沿边
沿边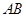 向上翻折,得到
向上翻折,得到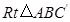 ,请求出
,请求出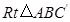 与矩形
与矩形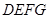 重叠部分的周长(可利用备用图).
重叠部分的周长(可利用备用图).
如图甲,分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为x轴、y轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在x轴上),抛物线y=14x2+bx+c经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
(1)求B点坐标;
(2)求证:ME是⊙P的切线;
(3)设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,①求△ACQ周长的最小值;
②若FQ=t,S△ACQ=S,直接写出S与t之间的函数关系式.
抛物线 的图像于x轴交于点M
的图像于x轴交于点M ,N
,N ,且经过点A(0,1),其中
,且经过点A(0,1),其中 ,过点A的直线
,过点A的直线 交x轴于C点,与抛物线交于点B(异于A点),满足△CAN是等腰直角三角形,切
交x轴于C点,与抛物线交于点B(异于A点),满足△CAN是等腰直角三角形,切 ,求解析式.
,求解析式.
(本题10分)问题情境


已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
| x |
…… |
 |
 |
 |
1 |
2 |
3 |
4 |
…… |
| y |
…… |
|
|
|
|
|
|
|
…… |

|
②观察图象,试描述该函数的增减性(y随x变化发生什么变化);
③在求二次函数y=ax+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC= ,直线y=
,直线y= 经过点C,交y轴于点G,且∠AGO=30°。
经过点C,交y轴于点G,且∠AGO=30°。
(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y= 上且经过点C、D的抛物线的解析式;
上且经过点C、D的抛物线的解析式;
(3)将(2)中的抛物线沿直线y= 平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存
平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存 在,请求出此时抛物线的解析式;若不存在,请说明理由。
在,请求出此时抛物线的解析式;若不存在,请说明理由。
(满分l4分)已知:抛物线y=x2-(a+2)x+9的顶点在坐标轴上.
(1)求a的值;
(2)若该抛物线的顶点C在x轴的正半轴上,而此抛物线与直线Y=x+9交于A,B两点,且A点在B点左侧,P为线段AB上的点(A,B两端点除外).过点P作x轴的垂线与抛物线交于点Q(可在图中画示意图).问:
①线段AB上是否存在这样的点P,使得PQ的长等于6?若存在,请求出点P的坐标;若不存在,请说明理由.
②线段AB上是否存在这样的点P,使得△ABQ∽△OAC?若存在,请求出此时点Q的坐标;若不存在,请说明理由.
如图甲,Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动(如图乙),直到C点与N点重合为止.设移动x秒后,矩形ABCD与△PMN重叠部分的面积为ycm2.求y与x之间的函数关系式.
(10分)恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放 天后,将这批香菇一次性出售,设这批香菇的销售总金额为
天后,将这批香菇一次性出售,设这批香菇的销售总金额为 元,试写出
元,试写出 与
与 之间的函数关系式.
之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
(本题10分) 已知一次函数y= 的图象与x轴交于点A.与
的图象与x轴交于点A.与 轴交于点
轴交于点 ;二次函数
;二次函数 图象与一次函数y=
图象与一次函数y= 的图象交于
的图象交于 、
、 两点,与
两点,与 轴交于
轴交于 、
、 两点且
两点且 的坐标为
的坐标为

(1)求二次函数的解析式;
(2)在 轴上是否存在点P,使得△
轴上是否存在点P,使得△ 是直角三角形?若存在,求出所有的点
是直角三角形?若存在,求出所有的点 ,若不存在,请说明理由。
,若不存在,请说明理由。
 |
|||||
 |
|||||
 |
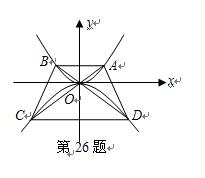
如图,点 在抛物线
在抛物线 上,过点
上,过点 作与
作与 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点 ,延长
,延长 分别与抛物线
分别与抛物线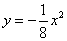 相交于点
相交于点 ,连接
,连接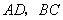 ,设点
,设点 的横坐标为
的横坐标为 ,且
,且 .
.
(1).当 时,求点
时,求点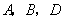 的坐标;
的坐标;
(2).当 为何值时,四边形
为何值时,四边形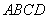 的两条对角线互相垂直;
的两条对角线互相垂直;
(3).猜想线段 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
﹣(本题12分)已知二次函数y=x2+bx+c与x轴交于A(-1,0)、B(1,0)两点.
(1)求这个二次函数的关系式;
(2)若有一半径为r的⊙P,且圆心P在抛物线上运动,当⊙P与两坐标轴都相切时,求半径r的值.
(3)半径为1的⊙P在抛物线上,当点P的纵坐标在什么范围内取值时,⊙P与y轴相离、相交?
如图,抛物线 (
( )与
)与 轴相交于
轴相交于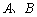 两点,点
两点,点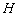 是抛物线的顶点,以
是抛物线的顶点,以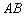 为直径作圆
为直径作圆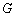 交
交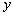 轴于
轴于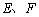 两点,
两点,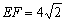 .
.
(1). 用含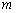 的代数式表示圆
的代数式表示圆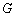 的半径
的半径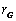 的长;
的长;
)
(2). 连结 ,求线段
,求线段 的长;
的长;
(3). 点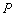 是抛物线对称轴正半轴上的一点,且满足以
是抛物线对称轴正半轴上的一点,且满足以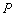 点为圆心的圆
点为圆心的圆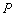 与直线
与直线 和圆
和圆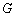 都相切,求点
都相切,求点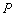 的坐标.
的坐标.
)
如图所示,将矩形 沿
沿 折叠,使点
折叠,使点 恰好落在
恰好落在 上
上 处,以
处,以 为边作正方形
为边作正方形 ,延长
,延长 至
至 ,使
,使 ,再以
,再以 、
、 为边作矩形
为边作矩形 .
.
(1). 试比较 、
、 的大小,并说明理由.
的大小,并说明理由.
2)令 ,请问
,请问 是否为定值?若是,请求出
是否为定值?若是,请求出 的值;若不是,请说明理由.
的值;若不是,请说明理由.
3在(2)的条件下,若 为
为 上一点且
上一点且 ,抛物线
,抛物线 经过
经过 、
、 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.
(4).在(3)的条件下,若抛物线 与线段
与线段 交于点
交于点 ,试问在直线
,试问在直线 上是否存在点
上是否存在点 ,使得以
,使得以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求直线
相似?若存在,请求直线 与
与 轴的交点
轴的交点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.