已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果:
①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0,
则正确的结论是( )

| A.①②③④ | B.②④⑤ | C.②③④ | D.①④⑤ |
抛物线y=3x2+2x﹣1向上平移4个单位长度后的函数解析式为( ).
| A.y=3x2+2x﹣5 | B.y=3x2+2x﹣4 |
| C.y=3x2+2x+3 | D.y=3x2+2x+4 |
“一般的,如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.--苏科版《数学》九年级(下册)P21”参考上述教材中的话,判断方程x2-2x= -2实数根的情况是( )
-2实数根的情况是( )
| A.有三个实数根 | B.有两个实数根 | C.有一个实数根 | D.无实数根 |
已知二次函数 自变量x与函数值y之间满足下列数量关系:
自变量x与函数值y之间满足下列数量关系:
| x |
2 |
4 |
5 |
| y |
0.37 |
0.37 |
4 |
那么 的值为( )
的值为( )
(A)24 (B)20 (C)10 (D)4
对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
| A.开口向下 |
| B.对称轴是x=-1 |
| C.顶点坐标是(1,2) |
| D.与x轴有两个交点 |
二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则a+b+1的值是( )
| A.﹣3 | B.﹣1 | C.2 | D.3 |
将函数y=x2+6x+7进行配方正确的结果应为( )
| A.y=(x+3)2+2 | B.y=(x-3)2+2 |
| C.y=(x+3)2-2 | D.y=(x-3)2-2 |
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )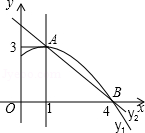
| A.①②③ | B.①③④ | C.①③⑤ | D.②④⑤ |
二次函数y=ax2+bx+c的图象如图所示,Q(n,2)是图象上的一点,且AQ⊥BQ,则a的值为( )
A.- |
B.- |
C.-1 | D.-2 |
抛物线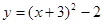 可以由抛物线
可以由抛物线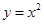 平移得到,则下列平移过程正确的是()
平移得到,则下列平移过程正确的是()
| A.先向左平移3个单位,再向上平移2个单位 |
| B.先向右平移3个单位,再向下平移2个单位 |
| C.先向左平移3个单位,再向下平移2个单位 |
| D.先向右平移3个单位,再向上平移2个单位[来 |
学生校服原来每套的售价是100元,后经连续两次降价,现在的售价是81元,则平均每次降价的百分数是 ( )
| A.9% | B.8.5% | C.9. 5% | D.10% |
抛物线 的顶点坐标是( )
的顶点坐标是( )
| A.(-2,-3) | B.(2,3) | C.(-2,3) | D.(2,-3) |
抛物线y=-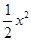 的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为( )
的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为( )
| A.(0,-2) | B.(0,2) | C.( -2,0) | D.(2,0) |