山东省聊城市阳谷县中考一模数学试卷

数轴上的点A到原点的距离是6，则点A表示的数为（ ）

如图，图中的几何体是圆柱沿竖直方向切掉一半后得到的，则该几何体的俯视图是（ ）

在一次“爱心互助”捐款活动中，某班第一小组8名同学捐款的金额（单位：元）如下表所示：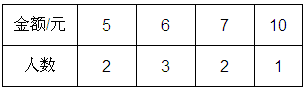

这8名同学捐款的平均金额为（     ）

如图，AB∥CD，AE交CD于C，∠A=34°，∠DEC=90°，则∠D的度数为（ ）

下列计算正确的（   ）

A．

B．

C．

D．

将函数y=x²+6x+7进行配方正确的结果应为（ ）

若∠AOB=45°，P是∠AOB内一点，分别作点P关于直线OA、OB的对称点P₁，P₂，连接OP₁，OP₂，则下列结论正确的是（ ）

A、OP₁⊥OP₂        B、OP₁=OP₂
C、OP₁≠OP²        D、OP₁⊥OP₂且OP₁=OP₂

“红灯停绿灯行”是我们在日常生活中必须遵守的交通规则，这样才能保障交通顺畅和行人安全．小刚每天从家骑自行车上学都经过三个路口，且每个路口安装了红灯和绿灯，假如每个路口红灯和绿灯亮的时间相同，那么小刚从家随时出发去学校，他遇到两次红灯的概率是（    ）

A．

B．

C．

D．

如图，在矩形ABCD中，边AB的长为3，点E，F分别在AD，BC上，连接BE，DF，EF，BD．若四边形BEDF是菱形，且EF=AE+FC，则边BC的长为（       ）

A、2      B、3         C、6        D、9  

已知点A（1，y₁）、B（2，y₂）、C（-3，y₃）都在反比例函数y＝的图象上，则y₁、y₂、y₃的大小关系是（  ）

若一个60°的角绕顶点旋转15°，则重叠部分的角的大小是（ ）     

二次函数y=ax²+bx+c的图象如图所示，它与x轴交于点（1，0），则化简二次根式的结果是（ ）

不等式组的解集是   ．

因式分解：x²-6x+9=            ．

如图，现有一圆心角为90°，半径为8cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为           cm．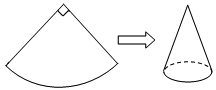

调查机构对某地区1000名20～30岁年龄段观众周五综艺节目的收视选择进行了调查，相关统计图如下，请根据图中信息，估计该地区20000名20～30岁年龄段观众选择观看《最强大脑》的人数约为            人．

如图，直线x=2与反比例函数y＝和y＝−的图象分别交于A、B两点，若点P是y轴上任意一点，则△PAB的面积是          
 

解分式方程:

李老师为了解班里学生的作息时间，调查了班上50名学生上学路上花费的时间，他发现学生所花时间都少于50分钟，然后将调查数据整理，作出如下频数分布直方图的一部分（每组数据含最小值不含最大值）．请根据该频数分布直方图，回答下列问题：

（1）此次调查的总体是什么？
（2）补全频数分布直方图；
（3）该班学生上学路上花费时间在30分钟以上（含30分钟）的人数占全班人数的百分比是多少？

如图，四边形ABCD是平行四边形，作AF∥CE，BE∥DF，AF交BE于G点，交DF于F点，CE交DF于H点、交BE于E点．
求证：△EBC≌△FDA．

某市为了改善市区交通状况，计划在康富路的北端修建通往资江北岸的新大桥，如图，新大桥的两端位于A、B两点，小张为了测量A、B之间的河宽，在垂直于新大桥AB的直线型道路l上测得如下数据：∠BDA=76．1°，∠BCA=68．2°，CD=82米．求：AB的长（精确到0．1米，参考数据：sin76．1°≈0．97，cos76．1°≈0．24，tan76．1°≈4．0；sin68．2°≈0．93，cos68．2°≈0．37，tan68．2°≈2．5）．

今年我区为绿化行车道，计划购买甲、乙两种树苗共计n棵．设买甲种树苗x棵．有关甲、乙两种树苗的信息如图所示．

（1）当n=500时，
①根据信息填表（用含x代数式表示）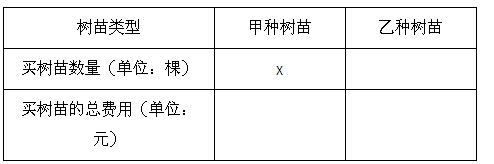

②如果购买甲、乙两种树苗共用25600元，那么甲、乙两种树苗各买了多少棵？
（2）要使这批树苗的成活率不低于92%，且使购买这两种树苗的总费用为26000元，求n的最大值．

已知：如图，△ABC中，以AB为直径的⊙O交AC于点D，且D为AC的中点，过D作DE丄CB，垂足为E．

（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）已知CD=4，CE=3，求⊙O的半径．

某校实行学案式教学，需印制若干份数学学案，印刷厂有甲、乙两种收费方式，除按印数收取印刷费外，甲种方式还需收取制版费而乙种不需要．两种印刷方式的费用y（元）与印刷份数x（份）之间的关系如图所示：

（1）填空：甲种收费的函数关系式是           ．
乙种收费的函数关系式是                ．  
（2）该校某年级每次需印制100～450（含100和450）份学案，选择哪种印刷方式较合算？

如图，矩形ABCD的两边长AB=18cm，AD=4cm，点P、Q分别从A、B同时出发，P在边AB上沿AB方向以每秒2cm的速度匀速运动，Q在边BC上沿BC方向以每秒1cm的速度匀速运动，当一点到达终点时，另一点也停止运动．设运动时间为x秒，△PBQ的面积为y（cm²）．

（1）求y关于x的函数关系式，并写出x的取值范围；
（2）求△PBQ的面积的最大值．