初中数学二次函数在给定区间上的最值试题

已知二次函数y=a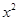+bx+c（a≠0）的图象如图所示，有下列结论：①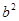－4ac＞0；②abc＞0；③b=-2a ④9a+3b+c＜0．其中，正确结论的个数是 （   ）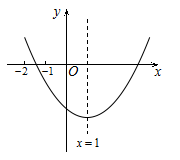

A．1

B．2

C．3

D．4

二次函数y＝ax²＋bx＋c（a≠0）的图象如图，下列结论正确的是（ ）
         

A．a<0

B．b^2－4ac<0

C．当－1<x<3时，y>0

D．－＝1

下列二次函数中，图象以直线x=2为对称轴、且经过点（0，1）的是 （    ）

A．y=+1	B．y=+1
C．y=－3	D．y=－3

对于抛物线y=ax²+bx+c（a≠0），有下列说法：
①当b=a+c时，则抛物线y=ax²+bx+c一定经过一个定点（-1，0）；
②若△=b²-4ac＞0，则抛物线y=cx²+bx+a与x轴必有两个不同的交点；
③若b=2a+3c，则抛物线y=ax²+bx+c与x轴必有两个不同的交点；
④若a＞0，b＞a+c，则抛物线y=ax²+bx+c与x轴必有两个不同的交点；
其中正确的有               ．

已知二次函数中，函数与自变量的部分对应值如下表：

	…	－2	－1	0	1	2	…
	…	－3	－4	－3	0	5	…

 
则此二次函数的对称轴为               ．

若抛物线与x轴分别交于A、B两点，且m为整数，则AB=_  _______．

已知抛物线的顶点在轴上，的值______________．

抛物线y=﹣x²+（m﹣1）x+m与y轴交于点（0，3）．
（1）求抛物线的解析式；
（2）求抛物线与坐标轴的交点坐标；
（3）①当x取什么值时，y＞0？②当x取什么值时，y的值随x的增大而减小？

用配方法将二次函数y=x²-2x+1写成y=a（x-h）²+k的形式是（   ）

A．y=（x-2）²-1	B．y=（x-1）²-1
C．y=（x-2）²-3	D．y=（x-1）²-3

二次函数y=x²的图象向上平移2个单位，得到新的图象的二次函数表达式是（    ）

A．y=x^2-2	B．y=（x-2）^2
C．y=x^2+2	D．y=（x+2）^2

关于抛物线y=(x-1)²-2，下列说法中错误的是

A．顶点坐标为(1，-2)

B．对称轴是直线x=1

C．当x＞1时，y随x的增大而减小

D．开口方向向上

二次函数y=-x²+2x+4的最大值为（ ）

A．3

B．4

C．5

D．6

关于二次函数y=（x-1）²+2，则下列说法正确的是（    ）

A．当x=1时，y有最大值为2

B．当x=1时，y有最小值为2

C．当x=-1时，y有最大值为2

D．当x=-1时，y有最小值为2

下列函数中，不属于二次函数的是（    ）

A．y=（x﹣2）^2	B．y=﹣2（x+1）（x﹣1）
C．y=1﹣x﹣x^2	D．y=

函数y=与y=-kx²+k（k≠0）在同一直角坐标系中的图象可能是（ ）