初中数学二次函数在给定区间上的最值试题

如图，已知抛物线经过，两点，顶点为．

（1）求抛物线的解析式；
（2）将绕点顺时针旋转90°后，点落到点的位置，  
将抛物线沿轴平移后经过点，求平移后所得图象的函数关系式；（3）设（2）中平移后，所得抛物线与轴的交点为，顶点为，若点在平移后的抛物线上，且满足的面积是面积的2倍，求点的坐标．

一快餐店试销某种套餐，试销一段时间后发现，每份套餐的成本为5元，该店每天固定支出费用为600元(不含套餐成本)．若每份售价不超过10元，每天可销售400份；若每份售价超过10元，每提高1元，每天的销售量就减少40份．为了便于结算，每份套餐的售价x(元)取整数，用y(元)表示该店日净收入．(日净收入＝每天的销售额－套餐成本－每天固定支出)
(1)求y与x的函数关系式；
(2)若每份套餐售价不超过10元，要使该店日净收入不少于800元，那么每份售价最少不低于多少元？
(3)该店既要吸引顾客，使每天销售量较大，又要有较高的日净收入．按此要求，每份套餐的售价应定为多少元？此时日净收入为多少？

抛物线的图象向右移动3个单位，再向下移动4个单位，它的解析式是   

把二次函数用配方法化成的形式（      ）    

A．

B．

C．

D．

如图，已知抛物线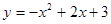与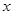轴的两个交点为A、B，与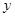轴交于点C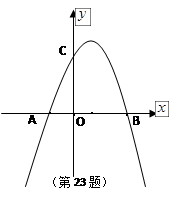

（1）求A、B、C三点的坐标？
（2）用配方法求该二次函数的对称轴和顶点坐标？
（3）若坐标平面内的点M，使得以点M和三点A、B、C为顶点的四边形是平行四边形，求点M的坐标？（直接写出M的坐标，不用说明）

一个二次函数的图象经过点（0，0），（-1，-1），（1，9）三点，求这个函数的关系式

点A是二次函数的图象上的一个点，写出一个
满足条件的A点的坐标是_______

嫦娥二号探月卫星于2010年10月1日发射成功。某科技实验小组也自行设计了火箭，经测试，该种火箭被竖直向上发射时，它的高度h (m)与时间t (s)的关系可以用公式表示．经过______s，火箭达到它的最高点．

已知二次函数的图象经过原点,与x轴的另一个交点为A, 抛物线的顶点为B,则△OAB的面积为    

如图，点A、B的坐标分别为（1, 4）和（4, 4）,一条抛物线与x轴交于C、D两点（C在D的左侧），它的顶点可在线段AB上运动，在运动过程中点C的横坐标最小值为，则点D的横坐标最大值为  (    )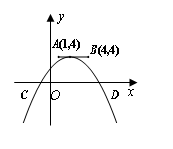

A．－3   　     B．1            C．5            D．8

二次函数的图象如图所示，则一次函数的
图象不经过()

A．第一象限

B．第二象限

C．第三象限

D．第四象限

二次函数的图象可由的图象（）

A．向左平移1个单位，再向下平移2个单位得到

B．向左平移1个单位，再向上平移2个单位得到

C．向右平移1个单位，再向下平移2个单位得到

D．向右平移1个单位，再向上平移2个单位得到

在抛物线上的一个点是（）

A．（4，4）

B．（1，－4）

C．（2，0）

D．（0，4）

下列各式中，y是x的二次函数的是()

A．

B．

C．

D．

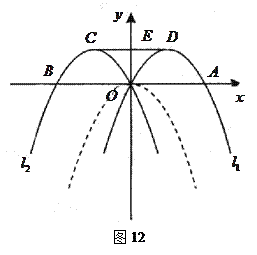
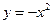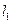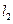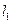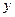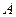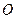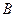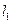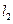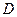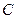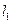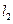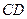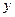如图12，把抛物线（虚线部分）向右平移1个单位长度，再向上平移1个单位长度，得到抛物线，抛物线与抛物线关于轴对称.点、、分别是抛物线、与轴的交点，、分别是抛物线、的顶点，线段交轴于点.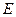

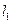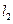（1）分别写出抛物线与的解析式；
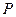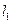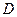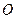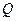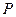（2）设是抛物线上与、两点不重合的任意一点，点是点关于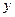轴的对称点，试判断以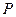、、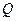、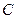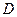为顶点的四边形是什么特殊的四边形？说明你的理由.
（3）在抛物线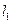上是否存在点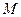，使得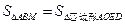，如果存在，求出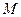点的坐标，如果不存在，请说明理由.