初中数学二次函数在给定区间上的最值试题

已知抛物线，当时，它的图象经过(        )

A．一、二、三象限	B．一、二、四象限
C．一、三、四象限	D．一、二、三、四象限.

把二次函数的图象向左平移2个单位，再向上平移1个单位，所得到的图象对应的二次函数关系式是（   ）

A．

B．

C．

D．

如果抛物线的顶点到轴的距离是3，那么的值等于（   ）

A．8

B．14

C．8或14

D．-8或-14

二次函数的最小值是（    ）．

A．2

B．1

C．－3

D．

二次函数，当时，随着的增大而增大，当时，随着的增大而减小，则的值应取（   ）

A．12

B．11

C．10

D．9

（本题8分）将二次函数y＝2x²－8x－5的图象沿它的对称轴所在直线向上平移，得到一条新的抛物线，这条新的抛物线与直线y＝kx＋1有一个交点为(3，4)．
　求：(1)新抛物线的解析式及后的值；
　　(2)新抛物线与y＝kx＋1的另一个交点的坐标．

当m＝   ▲   时，抛物线y＝x²－2mx＋4m＋1的顶点位置最高．

已知抛物线y＝x²－x－1与x轴的一个交点为(m，0)，则代数式m²－m＋2011的值是
   ▲   ．

抛物线y＝x²－x－2与坐标轴交点为点A、B、C，则AABC的面积为   ▲   ．

已知抛物线y＝－2x²＋4x－m的最大值为0，则m的值是   ▲   ．

已知二次函数y＝x²－4x＋3的图象是由y＝x²＋2x－1的图象先向上平移一个单位，再向

A．左移3个单位

B．右移3个单位

C．左移6个单位

D．右移6个单位

抛物线y＝x²－4x－7的顶点坐标是

A．（2，－11)

B．（－2，7)

C．(2，11)

D．（2，－3)

如图所示的是桥梁的两条钢缆具有相同的抛物线形状．按照图中建立的直角坐标系，右面的一条抛物线可以用y=0.0225x²－0.9x＋10表示，而且左右两条抛物线关于y轴对称，请你写出左面钢缆的表达式                。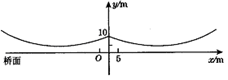

若A(－4，y₁)，B(－3，y₂），C(1，y₃)为二次函数y＝x²＋4x－5的图象上的三点，则y₁，y₂，y₃的大小关系是                                                (       )

A．y1< y2< y3

B．y2<y1<y3

C．y3<y1<y2

D．y1<y3< y2

二次函数的图象如何移动就得到的图象    （     ）

A．向右移动1个单位，向上移动4个单位

B．向左移动1个单位，向上移动4个单位

C．向右移动1个单位，向下移动4个单位

D．向左移动1个单位，向下移动4个单位