如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )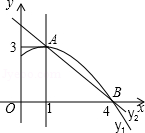
| A.①②③ | B.①③④ | C.①③⑤ | D.②④⑤ |
二次函数y=ax2+bx+c的图象如图所示,Q(n,2)是图象上的一点,且AQ⊥BQ,则a的值为( )
A.- |
B.- |
C.-1 | D.-2 |
抛物线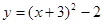 可以由抛物线
可以由抛物线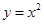 平移得到,则下列平移过程正确的是()
平移得到,则下列平移过程正确的是()
| A.先向左平移3个单位,再向上平移2个单位 |
| B.先向右平移3个单位,再向下平移2个单位 |
| C.先向左平移3个单位,再向下平移2个单位 |
| D.先向右平移3个单位,再向上平移2个单位[来 |
如图,抛物线y=-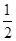 x2+bx+c与直线y=
x2+bx+c与直线y=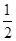 x+1交于A、B两点,点A在x轴上,点B的横坐标是2.点P在直线AB上方的抛物线上,过点P分别作PC∥y轴、PD∥x轴,与直线AB交于点C、D,以PC、PD为边作矩形PCQD,设点Q的坐标为(m,n).
x+1交于A、B两点,点A在x轴上,点B的横坐标是2.点P在直线AB上方的抛物线上,过点P分别作PC∥y轴、PD∥x轴,与直线AB交于点C、D,以PC、PD为边作矩形PCQD,设点Q的坐标为(m,n).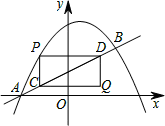
(1)点A的坐标是 ,点B的坐标是 ;
(2)求这条抛物线所对应的函数关系式;
(3)求m与n之间的函数关系式(不要求写出自变量n的取值范围);
(4)请直接写出矩形PCQD的周长最大时n的值.
学生校服原来每套的售价是100元,后经连续两次降价,现在的售价是81元,则平均每次降价的百分数是 ( )
| A.9% | B.8.5% | C.9. 5% | D.10% |
抛物线 的顶点坐标是( )
的顶点坐标是( )
| A.(-2,-3) | B.(2,3) | C.(-2,3) | D.(2,-3) |
抛物线y=-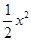 的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为( )
的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为( )
| A.(0,-2) | B.(0,2) | C.( -2,0) | D.(2,0) |
对于二次函数y=-x2+2x.有下列四个结论:
①它的对称轴是直线x=1;
②设y1=-x12 +2x1,y2=-x22+2x2,则当x2>x1时,有y2>y1;
③它的图象与x轴的两个交点是(0,0)和(2,0);
④当0<x<2时,y>0.
其中正确结论的个数为( )
| A.1 | B.2 | C.3 | D.4 |
对于二次函数 ,有下列说法:
,有下列说法:
①如果当x≤1时 随
随 的增大而减小,则m≥1;
的增大而减小,则m≥1;
②如果它的图象与x轴的两交点的距离是4,则 ;
;
③如果将它的图象向左平移3个单位后的函数的最小值是-4,则m=-1;
④如果当x=1时的函数值与x=2013时的函数值相等,则当x=2014时的函数值为-3.
其中正确的说法是 .
将抛物线y=2x2向左平移3个单位,再向上平移1个单位得到的抛物线表达式是( ).
A.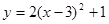 |
B.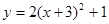 |
C.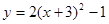 |
D.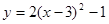 |
下列函数中,当x>0时,y值随x值增大而减小的是( ).
| A.y=x-3 | B.y=-3x2 | C.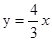 |
D.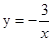 |