初中数学一元二次方程的最值试题

关于x的一元二次方程（a﹣6）x²﹣8x+9=0有实根．
（1）求a的最大整数值；
（2）当a取最大整数值时，①求出该方程的根；②求的值．

为建设美丽家园，某企业逐年增加对环境保护的经费投入，2012年投入了400万元，预计到2014年将投入576万元．
（1）求2012年至2014年该单位环保经费投入的年平均增长率；
（2）该单位预计2015年投入环保经费不低于680万元，若继续保持前两年的年平均增长率，该目标能否实现？请通过计算说明理由．

关于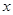的一元二次方程.
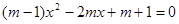（1）求证：方程有两个不相等的实数根；
（2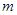）为何整数时，此方程的两个根都为正整数．

一家用电器开发公司研制出一种新型的电子产品，每件的生产成本为18元，按定价40元出售，每月可销售20万件．为了增加销售量，公司决定采取降价的办法，经市场调研，每降价1元，月销售量可增加2万件．
（1）求出月销售量y（万件）与销售单价x（元）之间的函数关系式（不必写出x的取值范围）；
（2）求出月销售利润z（万元）（利润＝售价－成本价）与销售单价x（元）之间的函数关系式（不必写出x的取值范围）．
（3）若某月利润为350万元时，则该月销售量为多少万件，此时销售单价为多少元？

电动自动车已成为市民日常出行的首选工具．据某市某品牌电动自行车经销商1至3月份统计，该品牌电动自行车1月份销售150辆，3月份销售216辆．
（1）求该品牌电动自行车销售量的月均增长率；
（2）若该品牌电动自行车的进价为2300元，售价为2800元，则该经销商1至3月共盈利多少元？

（本题12分）已知，如图，在平面直角坐标系中，点A、B的横坐标恰好是方程的解，点C的纵坐标恰好是方程的解，点P从C点出发沿y轴正方向以1个单位/秒的速度向上运动，连PA、PB，D为AC的中点.

1）求直线BC的解析式；
2）设点P运动的时间为t秒，问：当t为何值时，DP与DB垂直且相等？
3）如图2，若PA=AB，在第一象限内有一动点Q，连QA、QB、QP，且∠PQA=60°，问：当Q在第一象限内运动时，∠APQ+∠ABQ的度数和是否会发生改变？若不变，请说明理由并求其值.

（本题6分） 在2014年8月南京青奥会前夕，某体育用品店销售一批青奥会纪念品，平均每天可销售20件，每件赢利40元。为了扩大销售，该体育用品店决定采取适当降价措施。经调查发现，如果该青奥会纪念品每降价1元，该店平均每天可多售出2件。求：
（1）若该家体育用品店平均每天要赢利1200元，则这批青奥会纪念品应降价多少元？
（2）用配方法说明，每件青奥会纪念品降价多少元时，该家体育用品店平均每天赢利最多，最多是多少？

（本题6分）某养殖户每年的养殖成本包括固定成本和可变成本，其中固定成本每年均为4万元，可变成本逐年增长，已知该养殖户第1年的可变成本为2．6万元，设可变成本平均每年增长的百分率为x．
（1）用含x的代数式表示第3年的可变成本为     万元．
（2）如果该养殖户第3年的养殖成本为7．146万元，求可变成本平均每年增长的百分率

（10） 某西瓜经营户以2元/kg的价格购进一批小型西瓜，以3元/kg的价格出售，每天可售出200kg，为了尽快销售，该经营户决定降低销售价格，经调查发现，这种小型西瓜每降0．1元/kg ，每天可多售出40kg，另外，每天的房租等固定成本共24元，该经营户要想每天盈利200元，应将每千克小型西瓜的售价降低多少元？

商场某种商品平均每天可销售30件，每件盈利50元。为了尽快减少库存，商场决定采取适当的降价措施。经调查发现，每件商品每降价1元，商场平均每天可多售出2件。设每件商品降价x元。据此规律，请回答：
（1）商场日销售量增加       件，每件商品盈利       元（用含x的代数式表示）；
（2）在上述条件不变、销售正常情况下，每件商品降价多少元时，商场日盈利可达到2100元？

随着铁路运量的不断增长，重庆火车北站越来越拥挤，为了满足铁路交通的快速发展，该火车站从去年开始启动了扩建工程，其中某项工程，甲队单独完成所需时间比乙队单独完成所需时间多5个月，并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍。
（1）求甲、乙队单独完成这项工程各需几个月？
（2）若甲队每月的施工费为100万元，乙队每月的施工费比甲队多50万元，在保证工程质量的前提下，为了缩短工期，拟安排甲、乙两队分工合作完成这项工程。在完成这项工程中，甲队施工时间是乙队施工时间的2倍，那么，甲队最多施工几个月才能使工程款不超过1500万元？（甲、乙两队的施工时间按月取整数）

已知关于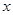的一元二次方程x²－4x＋k＋1＝0
（1）若=－1是方程的一个根，求k值和方程的另一根；
（2）设x₁，x₂是关于x的方程x²－4x＋k＋1＝0的两个实数根，是否存在实数k，使得x₁x₂＞x₁＋x₂成立？请说明理由．

对x，y定义一种新运算T，规定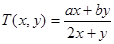：（其中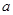、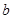均为非零常数），这里等式右边是通常的四则运算，例如：．
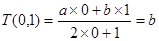（1）已知T（1，﹣1）=﹣2，T（4，2）=1．
①求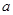、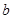的值；
②若关于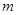的方程T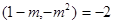有实数解，求实数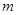的值；
（2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则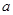、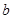应满足怎样的关系式？

如图，在平面直角坐标系中，Rt△ABC的斜边AB在x轴上，点C在y轴上，∠ACB=90°，OA、OB的长分别是一元二次方程x²﹣25x+144=0的两个根（OA＜OB），点D是线段BC上的一个动点（不与点B、C重合），过点D作直线DE⊥OB，垂足为E．

（1）求点C的坐标．
（2）连接AD，当AD平分∠CAB时，求直线AD的解析式．
（3）若点N在直线DE上，在坐标系平面内，是否存在这样的点M，使得C、B、N、M为顶点的四边形是正方形？若存在，请直接写出点M的坐标；若不存在，说明理由．

为满足市场需求，某超市在中秋节来临前夕，购进一种品牌月饼，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出1600盒，每盒售价每提高1元，每天要少卖出20盒．
（1）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？
（2）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得6000元的利润，那么超市每天销售月饼多少盒？