初中数学一元二次方程的最值解答题

某商店购进600个旅游纪念品，进价为每个6元，第一周以每个10元的价格售出200个，第二周若按每个10元的价格销售仍可售出200个，但商店为了适当增加销量，决定降价销售（根据市场调查，单价每降低1元，可多售出50个，但售价不得低于进价），单价降低x元，销售一周后，商店对剩余旅游纪念品清仓处理，以每个4元的价格全部售出，如果这批旅游纪念品共获利1250元．
（1）第二周单价降低x元后，这周销售的销量为       （用x的关系式表示）．
（2）求这批旅游纪念品第二周的销售价格．

某百货大搂服装柜在销售中发现：“七彩”牌童装平均每天可售出20件，每件盈利40元．为了迎接“元旦”，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件．
（1）要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？
（2）用配方法说明：要想盈利最多，每件童装应降价多少元？

随着人们环保意识的不断增强，我市家庭电动自行车的拥有量逐年增加．据统计，某小区2009年底拥有家庭电动自行车125辆，2011年底家庭电动自行车的拥有量达到180辆．
（1）若该小区2009年底到2012年底家庭电动自行车拥有量的年平均增长率相同，则该小区到2012年底电动自行车将达到多少辆？
（2）为了缓解停车矛盾，该小区决定投资3万元再建若干个停车位，据测算，建造费用分别为室内车位1000元/个，露天车位200元/个．考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的2.5倍，则该小区最多可建两种车位各多少个？试写出所有可能的方案．

现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．
（1）求该快递公司投递总件数的月平均增长率；
（2）如果平均每人每月最多可投递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？

已知关于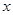的一元二次方程x²－4x＋k＋1＝0
（1）若=－1是方程的一个根，求k值和方程的另一根；
（2）设x₁，x₂是关于x的方程x²－4x＋k＋1＝0的两个实数根，是否存在实数k，使得x₁x₂＞x₁＋x₂成立？请说明理由．

佳佳超市经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，出售价格每涨价1元，日销售量将减少20千克，现佳佳超市要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？

解方程
（1）x²－10x=96 
（2）阅读下面的例题：
解方程x²-|x|－2=0．                       
解：分两种情况讨论：
①当x≥0时，原方程化为x²－x－2=0．
解得：x₁=2，x₂=－1(不合题意，舍去)；
②当x＜0时，原方程化为x²＋x－2=0．
解得：x₁=－2，x₂=1(不合题意，舍去)；
综上所述，原方程的根是x₁=2，x₂=－2．
请参照前面的例题的解法解方程：x²-|x－1|－1=0

解方程：
（1）x（x-2）=x-2；
（2）（x+8）（x+1）=-12．

某商场将某种商品的售价从原来的每件40元经两次调价后调至每件32.4元．
（1）若该商店两次调价的降价率相同，求这个降价率；
（2）经调查，该商品每降价0.2元，即可多销售10件．若该商品原来每月可销售500件，那么两次调价后，每月可销售该商品多少件？

对x，y定义一种新运算T，规定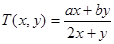：（其中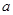、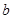均为非零常数），这里等式右边是通常的四则运算，例如：．
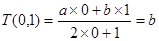（1）已知T（1，﹣1）=﹣2，T（4，2）=1．
①求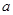、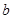的值；
②若关于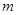的方程T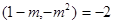有实数解，求实数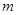的值；
（2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则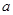、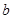应满足怎样的关系式？

为满足市场需求，某超市在中秋节来临前夕，购进一种品牌月饼，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出1600盒，每盒售价每提高1元，每天要少卖出20盒．
（1）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？
（2）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得6000元的利润，那么超市每天销售月饼多少盒？

某超市销售一种旅游纪念品，平均每天可售出20套，每套盈利40元．“十一”期间，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存．经市场调查发现：如果每套降价1元，那么平均每天就可多售出2套．要想平均每天销售这种纪念品盈利1200元，那么每套应降价多少元？

阅读下列例题：
解方程x²-|x|-2=0
解：（1）当x≥0时，原方程化为x²-x-2=0，解得x₁=2，x₂=-1（舍去）．
当x＜0时，原方程化为x²+x-2=0，解得x₁=1（舍去），x₂=-2．
∴x₁=2，x₂=-2是原方程的根．
请参照例题解方程：x²-|x-1|-1=0．

如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB），且OA、OB的长分别是一元二次方程x²-（＋1）x＋＝0的两个根．点C在x轴负半轴上，且AB：AC＝1：2．

（1）求A、C两点的坐标．
（2）若点M从点C出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围．
（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，说明理由．

我县某楼盘准备以每平方米4000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米3240元的均价开盘销售．
（1）求平均每次下调的百分率．
（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9．8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？