初中数学多元一次方程组试题

6个人用35天完成了某项工程的，如果再增加工作效率相同的8个人，那么完成这项工程，前后共用的天数是(    )

A．30

B．40

C．60

D．65

某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元．厂方在开展促销活动期间，向客户提供两种优惠方案：
①买一套西装送一条领带；
②西装和领带都按定价的90％付款．
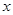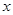现某客户要到该服装厂购买西装20套，领带条（>20）．
（1）若该客户按方案①购买，需付款________元（用含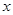的代数式表示）；若该客户按方案②购买，需付款________元（用含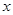的代数式表示）．
（2）若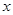=30，通过计算说明此时按哪种方案购买较为合算?

上海某宾馆客房部有三人普通间和二人普通间，每间收费标准如下表所示．世博会期间，一个由50名女工组成的旅游团人住该宾馆，她们都选择了三人普通间和二人普通间，且每间正好都住满．设该旅游团人住三人普通间有x间．
(1)该旅游团人住的二人普通间有________间(用含x的代数式表示)；
(2)该旅游团要求一天的住宿费必须少于4500元，且入住的三人普通间不多于二人普通间．若客房部能满
足该旅游团的要求，那么该客房部有哪几种安排方案?

客房	普通间(元／天)
三人间	240
二人间	200

已知、、…都是正整数，且，若的最大值为A，最小值为B，则A+B的值为__________

试验与探究：我们知道分数写为小数即，反之，无限循环小数 写成分数即.一般地，任何一个无限循环小数都可以写成分数形式.现在就以为例进行讨论：设 ，由…，可知，7.777… —0.777… =7，即 ,解方程得 于是得，.
请仿照上述例题完成下列各题：
（1）请你能把无限循环小数写成分数，即=       .
（2）你能化无限循环小数 为分数吗？请仿照上述例子求解之.

正值度尾文旦柚收成之际，在市场上直接销售，每吨利润为1000元，经粗加工后销售，每吨利润可达2000元；经精加工包装后销售，每吨利润为3000元．当地一家公司收购了600吨，该公司加工厂的生产能力是：如果对文旦柚进行粗加工，每天可加工50吨；如果进行精加工，每天可加工20吨，但每天两种方式不能同时进行，受季节条件的限制，公司必须在15天之内将这批文旦柚全部销售或加工完毕，为此公司研制了三种加工方案．
方案一：将文旦柚全部进行粗加工；
方案二：尽可能多的对文旦柚进行精加工，没有来得及加工的文旦柚在市场上直接销售；
方案三：将部分文旦柚进行精加工，其余文旦柚进行粗加工，并恰好在15天完成，
如果你是公司经理，你会选择哪种方案，说明理由。

在数学学习中，及时对知识进行归纳和整理是改善学习的重要方法．善于学习的小明在学习了一次方程（组）、一元一次不等式和一次函数后，把相关知识归纳整理如下：

（1）请你根据以上方框中的内容在下面数字序号后写出相应的结论：
①          ；②          ；③          ；④          ；
（2）如果点的坐标为（1，3），那么不等式的解集是          ．

在“家电下乡”活动期间，凡购买指定家用电器的农村居民均可得到每购买1元商品政府给予0.13元的财政补贴.村民小李购买了一台A型洗衣机，小王购买了一台B型洗衣机，两人一共得到财政补贴351元，又知B型洗衣机售价比A型洗衣机售价多500元.试求：
（1）A型洗衣机和B型洗衣机的售价各是多少元？
（2）小李和小王购买洗衣机除财政补贴外实际各付款多少元？

如图是某市民健身广场的平面示意图，它是由6个正方形拼成的长方形，已知中间最小的正方形A的边长是1米，
（1）若设图中最大正方形B的边长是x米，请用含x的代数式分别表示出正方形F、E和C的边长；
（2）观察图形的特点可知，长方形相对的两边是相等的（如图中的MN和PQ）．请根据这个等量关系，求出x的值；
（3）现沿着长方形广场的四条边铺设下水管道，由甲、乙2个工程队单独铺设分别需要10天、15天完成．如果两队从同一点开始，沿相反的方向同时施工2天后，因甲队另有任务，余下的工程由乙队单独施工，试问还要多少天完成？

甲杯中盛有红墨水若干ml，乙杯中盛有蓝墨水若干ml，现在用一个容积为50ml
的小杯子从甲杯中盛走一小杯红墨水倾入乙杯，待乙杯中两种墨水混合均匀后；从乙杯中盛
走一小杯混合液倾入甲杯中，试问，这时乙杯中的红墨水的液量和甲杯中混进来的蓝墨水的
液量相比，哪个多？

A．甲杯蓝墨水多，乙杯红墨水少	B．甲杯蓝墨水少，乙杯红墨水多
C．甲杯蓝墨水与乙杯红墨水一样多甲	D．无法判定

为了提升学生体育锻炼意识，某中学七年级(1)班进行了一次体育测试，测试内容为投掷实心球，老师在操场上画出了A，B，C三个区域，每人投掷5次，实心球落在各个区域的分值各不相同，落在C区得3分．墨墨，茗茗，丽丽三位同学投掷后其落点如图所示，已知墨墨的得分是19分．

（1）设投进B区域得x分，用整式表示投进A区域的得分；
（2）若茗茗的得分是21分，求投进B区域的得分；
（3）求丽丽的得分．

小明锻炼健身，从A地匀速步行到B地用时25分钟．若返回时，发现走一小路可使A、B两地间路程缩短200米，便抄小路以原速返回，结果比去时少用2．5分钟．
（1）求返回时A、B两地间的路程；
（2）若小明从A地步行到B地后，以跑步形式继续前进到C地（整个锻炼过程不休息）．据测试，在他整个锻炼过程的前30分钟（含第30分钟），步行平均每分钟消耗热量6卡路里，跑步平均每分钟消耗热量10卡路里；锻炼超过30分钟后，每多跑步1分钟，多跑的总时间内平均每分钟消耗的热量就增加1卡路里．测试结果，在整个锻炼过程中小明共消耗904卡路里热量．问：小明从A地到C地共锻炼多少分钟？

先阅读短文，然后回答短文后面所给出的问题：
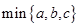对于三个数a、b、c的平均数，最小的数都可以给出符号来表示，我们规定 表示这三个数的平均数，表示这三个数中的最小的数，表示这三个数中最大的数．例如：，，；，．
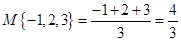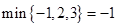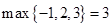（1）请填空：      ；若，则      ；
（2）若，求的取值范围；
（3）若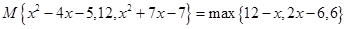，求的值．

如图，点A从原点出发沿数轴向左运动，同时，点B也从原点出发沿数轴向右运动，3秒后，两点相距15个单位长度．已知点B的速度是点A的速度的4倍（速度单位：单位长度/秒）．

（1）求出点A、点B运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置；
（2）若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动，几秒时，原点恰好处在点A、点B的正中间？
（3）若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动时，另一点C同时从B点位置出发向A点运动，当遇到A点后，立即返回向B点运动，遇到B点后又立即返回向A点运动，如此往返，直到B点追上A点时，C点立即停止运动．若点C一直以20单位长度/秒的速度匀速运动，那么点C从开始运动到停止运动，行驶的路程是多少个单位长度？