2015年5月,我市某中学举行了“中国梦•校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,并绘制了不完整的两种统计图.
根据图中提供的信息,回答下列问题:
(1)参加演讲比赛的学生共有人,并把条形图补充完整;
(2)扇形统计图中,m=,n=;C等级对应扇形的圆心角为度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树形图法,求获A等级的小明参加市比赛的概率.
我区实施新课程改革后,学生的自主字习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调査,并将调査结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调査结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,张老师一共调査了名同学,其中C类女生有名,D类男生有名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B 布袋中有三个完全相同的小球,分别标有数字-1,-2和-3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为 .
.
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在抛物线y=x2-2x-1上的概率.
.某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
完全相同的4个小球,上面分别标有数字1、-1、2、-2,将其放入一个不透明的盒子中摇匀,再从中随机摸球两次.把第一次、第二次摸到的球上标有的数字分别记作m、n,以m、n分别作为一个点的横坐标与纵坐标,
(1)若第一次摸出球后放回摇匀,求点(m,n)不在第二象限的概率.(用列表法求解)
(2)若第一次摸出球后不放回,求点(m,n)不在第二象限的概率.(用树状图求解)
在一个不透明的口袋中有四个手感完全一致的小球,四个小球上分别标有数字-4,-1, 2, 5;
(1)从口袋中随机摸出一个小球,其上标明的数是奇数的概率是多少?
(2)从口袋中随机摸出一个小球不放回,再从中摸出第二个小球:
①请用表格或树状图表示先后摸出的两个小球所标数字组成的可能结果?
②求依次摸出的两个小球所标数字为横坐标,纵坐标的点位于第四象限的概率.
设点A的坐标(x,y),其中横坐标x可取-1,2,纵坐标y可取-1,1,2。
(1)求出点A的坐标的所有等可能结果(用树形图或列表法求解);
(2)求点A与点B(1,-1)关于原点对称的概率。
三个小球分别标有﹣2,0,1三个数,这三个球除了标的数不同外,其余均相同,将小球放入一个不透明的布袋中搅匀.
(1)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸出一个小球,再记下小球上所标之数,求两次记下之数的和大于0的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
(2)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸出一个小球,将小球上所标之数再记下,…,这样一共摸了13次.若记下的13个数之和等于﹣4,平方和等于14.求:这13次摸球中,摸到球上所标之数是0的次数.
以下四个命题:
①每一条对角线都平分一组对角的平行四边形是菱形.
②当m > 0时, y =–mx+1与 两个函数都是y随着x的增大而减小.
两个函数都是y随着x的增大而减小.
③已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若A点坐标为(1, )则D点坐标为(1,
)则D点坐标为(1, ).
).
④在一个不透明的袋子中装有标号为1,2,3,4的四个完全相同的小球,从袋中随机摸取一个然后放回,再从袋中随机地摸取一个,则两次取到的小球标号的和等于4的概率为 .
.
其中正确的命题有(只需填正确命题的序号)
有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6),以小莉掷A立方体朝上的数字为x、小明掷B立方体朝上的数字为y来确定点P(x,y),那么他们各掷一次所确定的点P落在抛物线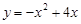 上的概率为( )
上的概率为( )
A.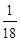 B.
B.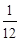 C.
C.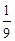 D.
D.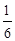
有三张正面分别写有数字﹣2,﹣1,1的卡片,它们的背面完全相同,将这三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y).
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式 有意义的(x,y)出现的概率
有意义的(x,y)出现的概率
有四张正面分别标有数字-2,-1,1,2的不透明卡片,它们除数字不同外其余相同。现将它们背面朝上,洗匀后小李从中任取两张,将该卡片上的数字这和记为x,则小李得到的x值使分式 的值为0的概率是________.
的值为0的概率是________.
小张的三位朋友甲、乙、丙想破译他在电脑中设置的登录密码.但是他们只知道这个密码共有五位数字.他们根据小张平时开电脑时输入密码的手势,分别猜测密码是“51932”、“85778”或“74906”.实际上他们每个人都只猜对了密码中对应位置不相邻的两个数字.由此你知道小张设置的密码是________.
在平面直角坐标系中,作△OAB,其中三个顶点分别为O(0,0),B(1,1)A(x,y)( 均为整数),则所作△OAB为直角三角形的概率是。
均为整数),则所作△OAB为直角三角形的概率是。