2015年5月，我市某中学举行了“中国梦•校园好少年”演讲比赛活动，根据学生的成绩划分为A，B，C，D四个等级，并绘制了不完整的两种统计图．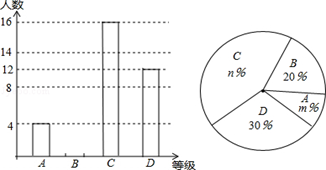
根据图中提供的信息，回答下列问题：
（1）参加演讲比赛的学生共有 人，并把条形图补充完整；
（2）扇形统计图中，m= ，n= ；C等级对应扇形的圆心角为 度；
（3）学校欲从获A等级的学生中随机选取2人，参加市举办的演讲比赛，请利用列表法或树形图法，求获A等级的小明参加市比赛的概率．
相关试题
、
的式子表示图中阴影部分的面积；
，
时求图中阴影部分的面积．
小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分)，请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子．
注意：只需添加一个符合要求的正方形，并用阴影表示．
，化简 
再求值．相关知识点
推荐套卷
粤公网安备 44130202000953号