初中数学概率公式试题

如果任意选择一对有序整数 $(m,n)$，其中 $\left|m\right|⩽1$， $\left|n\right|⩽3$，每一对这样的有序整数被选择的可能性是相等的，那么关于 $x$的方程 $x^2+\mathit{nx}+m=0$有两个相等实数根的概率是　　．

如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分，现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表面展开图的概率是 $($　　 $)$

A． $\frac{4}{7}$B． $\frac{3}{7}$C． $\frac{2}{7}$D． $\frac{1}{7}$

为了传承优秀传统文化，某校开展“经典诵读”比赛活动，诵读材料有《论语》，《三字经》，《弟子规》（分别用字母 $A$， $B$， $C$依次表示这三个诵读材料），将 $A$， $B$， $C$这三个字母分别写在3张完全相同的不透明卡片的正面上，把这3张卡片背面朝上洗匀后放在桌面上．小明和小亮参加诵读比赛，比赛时小明先从中随机抽取一张卡片，记录下卡片上的内容，放回后洗匀，再由小亮从中随机抽取一张卡片，选手按各自抽取的卡片上的内容进行诵读比赛．

（1）小明诵读《论语》的概率是　　；

（2）请用列表法或画树状图（树形图）法求小明和小亮诵读两个不同材料的概率．

现有3张正面图形分别是等边三角形、平行四边形、正方形的卡片，它们除正面图形不同，其他完全相同，将它们背面朝上洗匀后，从中随机抽取1张卡片，卡片的正面图形是中心对称图形的概率是 $($　　 $)$

A． $\frac{1}{3}$B． $\frac{2}{3}$C． $\frac{1}{6}$D． $\frac{5}{6}$

九年一班组织班级联欢会，最后进入抽奖环节，每名同学都有一次抽奖机会，小强拿出一个箱子说：“这个不透明的箱子里装有红、白球各1个和若干个黄球，它们除了颜色外其余都相同，谁能同时摸出两个黄球谁就获得一等奖”．已知任意摸出一个球是黄球的概率为 $\frac{1}{2}$．

（1）请直接写出箱子里有黄球　　个；

（2）请用列表或树状图求获得一等奖的概率．

在一个不透明的布袋中装有若干个只有颜色不同的小球，如果袋中有红球5个，黄球4个，其余为白球，从袋子中随机摸出一个球，“摸出黄球”的概率为 $\frac{1}{3}$，则袋中白球的个数为 $($　　 $)$

A．2B．3C．4D．12

在一个不透明的袋子中装有除颜色外其他均相同的3个红球和2个白球，从中任意摸出一个球，则摸出白球的概率是　　．

某校九年二班在体育加试中全班所有学生的得分情况如表所示：

分数段（分 $)$	$15-19$	$20-24$	$25-29$	30
人数	1	5	9	25

从九年二班的学生中随机抽取一人，恰好是获得30分的学生的概率为　　．

一个袋中装有两个红球、三个白球，每个球除颜色外都相同．从中任意摸出一个球，摸到红球的概率是　　．

有五张背面完全相同的卡片，正面分别写有 $\sqrt{9}$， ${\left(\sqrt{2}\right)}^0$， $\sqrt{8}$， $\frac{22}{7}$， $2^{-2}$，把卡片背面朝上洗匀后，从中随机抽取一张，其正面的数字是无理数的概率是 $($　　 $)$

A． $\frac{1}{5}$B． $\frac{2}{5}$C． $\frac{3}{5}$D． $\frac{4}{5}$

某同学报名参加校运动会，有以下4个项目可选择．

径赛项目： $100m$跑， $200m$跑， $400m$跑（分别用 $A_1$， $A_2$， $A_3$表示． $)$田赛项目：跳远（用 $B$表示）．

（1）该同学从4个项目中任选1个是径赛项目的概率为　．

（2）该同学从4个项目中任选2个，请用画树状图或列表的方法列举出所有可能出现的结果，并求参赛项目都是径赛的概率．

如图，有四张背面完全相同的纸牌 $A$、 $B$、 $C$、 $D$，其正面分别画有四个不同的几何图形，将这四张纸牌背面朝上洗匀．

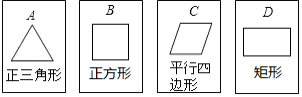
（1）从中随机摸出一张，求摸出的牌面图形是中心对称图形的概率；

（2）小明和小亮约定做一个游戏，其规则为：先由小明随机摸出一张纸牌，不放回，再由小亮从剩下的纸牌中随机摸出一张，若摸出的两张牌面图形都是轴对称图形小明获胜，否则小亮获胜，这个游戏公平吗？请用列表法（或树状图）说明理由（纸牌用 $A$、 $B$、 $C$、 $D$表示）．

从数 $-2$，1，2，5，8中任取一个数记作 $k$，则正比例函数 $y=\mathit{kx}$的图象经过第二、四象限的概率是　　．

对于 $▱\mathit{ABCD}$，从以下五个关系式中任取一个作为条件：① $\mathit{AB}=\mathit{BC}$；② $\angle \mathit{BAD}=90°$；③ $\mathit{AC}=\mathit{BD}$；④ $\mathit{AC}\perp \mathit{BD}$；⑤ $\angle \mathit{DAB}=\angle \mathit{ABC}$，能判定 $▱\mathit{ABCD}$是矩形的概率是　　．

现有五张正面图形分别是平行四边形、圆、等边三角形、正五边形、菱形的卡片，它们除正面图形不同，其它完全相同．将它们背面朝上洗匀后，从中随机抽取一张卡片，卡片的正面图形既是中心对称图形又是轴对称图形的概率是　　．