初中数学统计量的选择试题

有4张形状、大小和质地都相同的卡片，正面分别写有字母A、B、C、D和一个算式，背面完全一致．如图所示，将这4张卡片背面向上洗匀，从中随机抽取1张，不放回，接着再随机抽取1张．

（1）请用画树形图或列表法表示出所有的可能结果；（卡片可用A、B、C、D表示）
（2）将“第一张卡片上的算式是正确，同时第二张卡片上的算式是错误”记为事件A，求事件A的概率．

某校开展了以“人生观、价值观”为主题的班队活动，活动结束后，九(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查（要求每位同学只选自己最认可的一项观点），并制成了如下扇形统计图．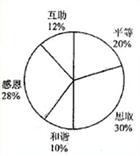

（1）该班学生选择“互助”观点的有       人，在扇形统计图中，“和谐”观点所在扇形区域的圆心角是      度；
（2）如果该校有1500名九年级学生，利用样本估计选择“感恩”观点的九年级学生约有__420____人．
（3）如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查，求恰好选到“和谐”和“感恩”观点的概率．（用树状图或列表法分析解答）

PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．根据PM2.5检测网的空气质量新标准，从德州市2013年全年每天的PM2.5日均值标准值（单位：微克/立方米）监测数据中随机地抽取25天的数据作为样本，并根据检测数据制作了尚不完整的频数分布表和条形图：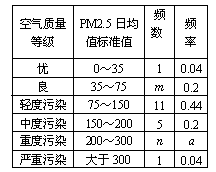
       
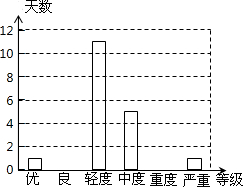
（1）求出表中m，n，a的值，并将条形图补充完整；
（2）以这25天的PM2.5日均值来估计该年的空气质量情况，估计该年(365天)大约有多少天的空气质量达到优或良；
（3）请你结合图表评价一下我市的空气质量情况．

减负提质“1＋5”行动计划是我市教育改革的一项重要举措。某中学“阅读与演讲社团”为了了解本校学生的每周课外阅读时间，采用随机抽样的方法进行了问卷调查，调查结果分为“2小时以内”、“2小时～3小时”、“3小时～4小时”、“4小时以上”四个等级，分别用A、B、C、D表示，根据调查结果绘制成了如图的两幅不完整的统计图。由图中给出的信息解答下列问题：

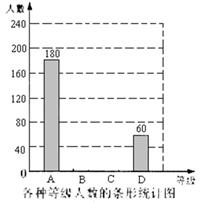
（1）求出x的值，并将不完整的条形统计图补充完整；
（2）在此次调查活动中，初三（1）班的两个学习小组各有2人每周阅读时间都是4小时以上，现从中任选2 人去参加学校的知识抢答赛。用列表或画树状图的方法求选出的2人来自不同小组的概率。

2014年郑州市城镇民营企业就业人数突破20万，为了解城镇民营企业员工每月的收入状况，统计局对全市城镇企业民营员工2014年月平均收入随机抽样调查，将抽样的数据按“2000元以内”、“2000元～4000元”、“4000元～6000元”和“6000元以上”分为四组，进行整理，分别用A，B，C，D表示，得到下列两幅不完整的统计图．

由图中所给出的信息解答下列问题：
（1）本次抽样调查的员工有_____人，在扇形统计图中x的值为_____，表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是_____；
（2）将不完整的条形图补充完整，并估计我市2013年城镇民营企业20万员工中，每月的收入在“2000元～4000元”的约多少人？
（3）统计局根据抽样数据计算得到，2013年我市城镇民营企业员工月平均收入为4872元，请你结合上述统计的数据，谈一谈用平均数反映月收入情况是否合理？

某个体户以每件80元的价格进了一种服装100件，用五天的时间售完．在销售过程中，发现由于每天销售的价格不同，所销售的件数就不一样（如图所示）.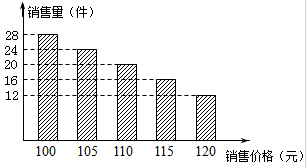

另外，每天的支出情况见下表：

日支出项目	房租	税收	员工工资	其他
日支出金额（元）	100	60	90	30

 
根据图表提供的信息，回答下列问题：
（1）销售价是110元的这一天，卖了多少件？除去所有开支和进货成本，净赚了多少元？
（2）卖完100件这种服装后，除去5天的开支和进货的成本，共净赚了多少元？

嘉兴市2010~2014年社会消费品零售总额及增速统计图如下：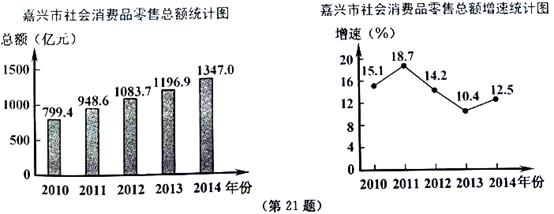

请根据图中信息，解答下列问题：
（1）求嘉兴市2010~2014年社会消费品零售总额增速这组数据的中位数．
（2）求嘉兴市近三年（2012~2014年）的社会消费品零售总额这组数据的平均数．
（3）用适当的方法预测嘉兴市2015年社会消费品零售总额（只要求列出算式，不必计算出结果）．

某学校为了解本校学生课外阅读的情况，从全体学生中随机抽取了部分学生进行调查，并将调查结果绘制成右图统计表．已知该校全体学生人数为1200人，由此可以估计每周课外阅读时间在1~2（不含1）小时的学生有_________人．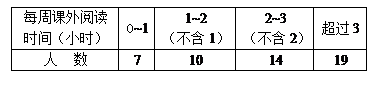

某高中学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查，并根据调查结果绘制了如图两个不完整的统计图（校服型号以身高作为标准，共分为6种型号）

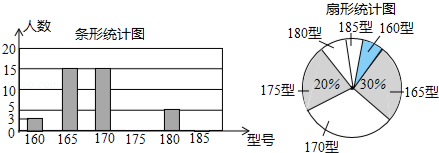
根据以上信息，解答下列问题：
（1）该班共有   名学生，其中穿175型校服的学生有   名．
（2）在条形统计图中，请把空缺部分补充完整．
（3）该班学生所穿校服型号的众数为       ，中位数为     ．

(本题8分)王大伯几年前承包了甲、乙两片荒山，各栽100棵杨梅树，成活98%．现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了4棵树上的杨梅，每棵的产量如折线统计图所示.
（1）分别计算甲、乙两山样本的平均数，并估算出甲、乙两山杨梅的产量总和；
（2）试通过计算说明，哪个山上的杨梅产量较稳定？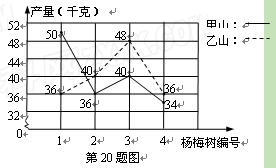

多多班长统计去年1～8月“书香校园”活动中全班同学的课外阅读数量（单位：本），绘制了如图折线统计图，下列说法正确的是（　　）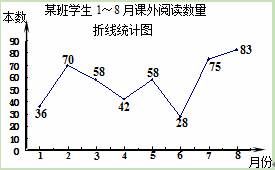

A．极差是47	B．众数是42
C．中位数是58	D．每月阅读数量超过40的有4个月

某校组织初三学生电脑技能竞赛，每班参加比赛的学生人数相同，竞赛成绩分为A、B、C、D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分．将初三(1)班和(2)班的成绩整理并绘制成统计图如下．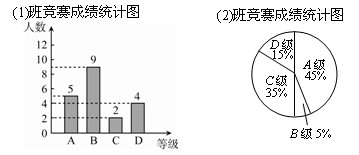

（1）此次竞赛中（2）班成绩在C级以上（包括C级）的人数为       ；

	平均数	中位数	众数
（1）班		90	90
（2）班	88		100

（2）请你将表格补充完整：
（3）试运用所学的统计知识，从二个不同角度评价初三（1）班和初三（2）班的成绩．

为了解某校九年级学生体育模考情况，现从中随机抽取部分学生的体育模考成绩统计如下，其中扇形统计图中的圆心角α为36°．
九年级学生体育模考成绩统计表

体育成绩	人数（人）	百分比（%）
26
27	m
28	8	16
29		24
30	15

根据上面提供的信息，回答下列问题：
（1）m＝     ；抽取的部分学生体育模考成绩的中位数为   ；
（2）已知该校九年级共有500名学生，如果体育模考成绩达29分（含29分）为优秀，请估计该校九年级学生体育模考成绩达到优秀的总人数．

甲、乙两名同学某学期的四次数学测试成绩（单位：分）如下表：

据上表计算，甲、乙两名同学四次数学测试成绩的方差分别为，，下列说法正确的是（ ）

A．甲同学四次数学测试成绩的平均数是89分

B．甲同学四次数学测试成绩的中位数是90分

C．乙同学四次数学测试成绩的众数是80分

D．乙同学四次数学测试成绩较稳定

省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

	第一次	第二次	第三次	第四次	第五次	第六次
甲	10	8	9	8	10	9
乙	10	7	10	10	9	8

根据表格中的数据，已经求出甲六次测试的平均成绩=9环，方差=．
（1）计算乙六次测试的平均成绩及方差；
（2）你认为推荐谁参加全国比赛更合适？请说明理由．
（提示：[（x₁-）²+（x₂-）²+…+（x_n-）²]）