某校组织初三学生电脑技能竞赛,每班参加比赛的学生人数相同,竞赛成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.将初三(1)班和(2)班的成绩整理并绘制成统计图如下.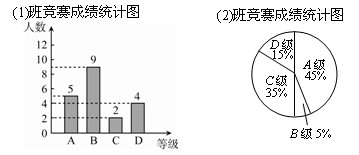
(1)此次竞赛中(2)班成绩在C级以上(包括C级)的人数为 ;
| |
平均数 |
中位数 |
众数 |
| (1)班 |
|
90 |
90 |
| (2)班 |
88 |
|
100 |
(2)请你将表格补充完整:
(3)试运用所学的统计知识,从二个不同角度评价初三(1)班和初三(2)班的成绩.
2013年起,深圳市实施行人闯红灯违法处罚,处罚方式分为四类:“罚款20元”、“罚款50元”、“罚款100元”、“穿绿马甲维护交通”。下图是实施首日由某片区的执法结果整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:

(1)实施首日,该片区行人闯红灯违法受处罚一共 人;
(2)在所有闯红灯违法受处罚的行人中,穿绿马甲维护交通所占的百分比是 %;
(3)据了解,“罚款20元”人数是“罚款50元”人数的2倍,请补全条形统计图;
(4)根据(3)中的信息,在扇形统计图中,“罚款20元”所在扇形的圆心角等于 度。
第九届中国国际园林博览会(园博会)已于2013年5月18日在北京开幕,以下是根据近几届园博会的相关数据绘制的统计图的一部分: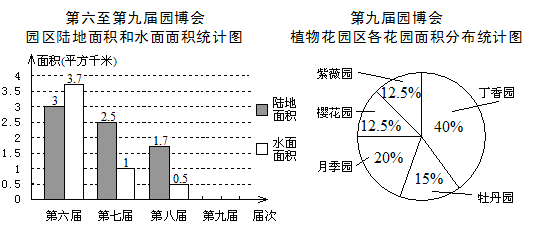
(1)第九届园博会的植物花园区由五个花园组成,其中月季园面积为0.04平方千米,牡丹园面积为 平方千米;
(2)第九届园博会园区陆地面积是植物花园区总面积的18倍,水面面积是第七、八两届园博会的水面面积之和,请根据上述信息补全条形统计图,并标明相应数据;
(3)小娜收集了几届园博会的相关信息(如下表),发现园博会园区周边设置的停车位数量与日接待游客量和单日最多接待游客量中的某个量近似成正比例关系,根据小娜的发现,请估计将于2015年举办的第十届园博会大约需要设置的停车位数量(直接写出结果,精确到百位)。
第七届至第十届园博会游客量与停车位数量统计表
| |
日均接待游客量(万人次) |
单日最多接待游客量(万人次) |
停车位数量(个) |
| 第七届 |
0.8 |
6 |
约3 000 |
| 第八届 |
2.3 |
8.2 |
约4 000 |
| 第九届 |
8(预计) |
20(预计) |
约10 500 |
| 第十届 |
1.9(预计) |
7.4(预计) |
约 . |
初中生对待学习的态度一直是教育工作者关注的问题之一.为此无锡市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
吴老师为了解本班学生的数学学习情况,对某次数学考试成绩(成绩取整数,满分为100分)作了统计,绘制成如下频数分布表和频数分布直方图.
请你根据图表提供的信息,解答下列问题:
(1)求频率分布表中 、
、 、
、 的值;并补全频数分布直方图;
的值;并补全频数分布直方图;
(2)如果用扇形统计图表示这次数学考试成绩时,那么成绩在69.5~79.5范围内的扇形圆心角的度数为多少度?
| 分组 |
49.5~59.5 |
59.5~69.5 |
69.5~79.5 |
79.5~89.5 |
89.5~100.5 |
合计 |
| 频数 |
3 |
 |
10 |
26 |
6 |
 |
| 频率 |
0.06 |
0.10 |
0.20 |
0.52 |
 |
1.00 |

为了解某校九年级学生体育模考情况,现从中随机抽取部分学生的体育模考成绩统计如下,其中扇形统计图中的圆心角α为36°.
九年级学生体育模考成绩统计表
| 体育成绩 |
人数(人) |
百分比(%) |
| 26 |
|
|
| 27 |
m |
|
| 28 |
8 |
16 |
| 29 |
|
24 |
| 30 |
15 |
|

根据上面提供的信息,回答下列问题:
(1)m= ;抽取的部分学生体育模考成绩的中位数为 ;
(2)已知该校九年级共有500名学生,如果体育模考成绩达29分(含29分)为优秀,请估计该校九年级学生体育模考成绩达到优秀的总人数.
(本题8分)仪征市某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式” 随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:
(1)这次抽样调查中,共调查了 名学生;
(2)补全两幅统计图;
(3)根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?
某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号)
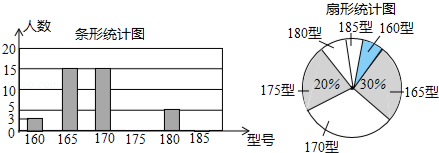
根据以上信息,解答下列问题:
(1)该班共有 名学生,其中穿175型校服的学生有 名.
(2)在条形统计图中,请把空缺部分补充完整.
(3)该班学生所穿校服型号的众数为 ,中位数为 .
甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为 ,
, ,下列说法正确的是( )
,下列说法正确的是( )
| A.甲同学四次数学测试成绩的平均数是89分 |
| B.甲同学四次数学测试成绩的中位数是90分 |
| C.乙同学四次数学测试成绩的众数是80分 |
| D.乙同学四次数学测试成绩较稳定 |
生物学研究表明,在8﹣﹣17岁期间,男女生身高增长速度规律呈现如下图所示,请你观察此图,回答下列问题,男生身高增长速度的巅峰是几岁?在几岁时男生、女生的身高增长速度是一样的?
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加.按团体总分多少排列名次,在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个),经统计发现两班总分相等,此时有学生建议,可通过考查数据中的其他信息作为参考.请你回答下列问题:
| |
1号 |
2号 |
3号 |
4号 |
5号 |
总分 |
| 甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
| 乙班 |
86 |
100 |
98 |
119 |
97 |
500 |
(1)根据上表提供的数据填写下表:
| |
优秀率 |
中位数 |
方差 |
| 甲班 |
|
|
|
| 乙班 |
|
|
|
(2)根据以上信息,你认为应该把冠军奖状发给哪一个班级? 简述理由.
近几年,丹东市加大中职教育投入力度,取得了良好的社会效果,某学校随机调查了九年级m名学生的升学意向,并根据结果绘制出如下两幅不完整的统计图,请根据图中信息解答下列问题
(1)m=
(2)扇形统计图中“职高”对应的扇形圆心角=
(3)补全条形统计图
(4)若该校九年级学生有900人,估计该校共有多少名毕业生的升学意向是职高?
|


2014年郑州市城镇民营企业就业人数突破20万,为了解城镇民营企业员工每月的收入状况,统计局对全市城镇企业民营员工2014年月平均收入随机抽样调查,将抽样的数据按“2000元以内”、“2000元~4000元”、“4000元~6000元”和“6000元以上”分为四组,进行整理,分别用A,B,C,D表示,得到下列两幅不完整的统计图.
由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有_____人,在扇形统计图中x的值为_____,表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是_____;
(2)将不完整的条形图补充完整,并估计我市2013年城镇民营企业20万员工中,每月的收入在“2000元~4000元”的约多少人?
(3)统计局根据抽样数据计算得到,2013年我市城镇民营企业员工月平均收入为4872元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论正确的是( )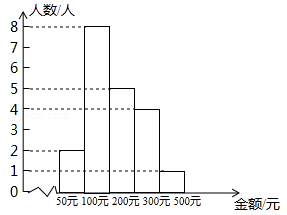
| A.样本中位数是200元 |
| B.样本容量是20 |
| C.该企业员工捐款金额的极差是450元 |
| D.该企业员工最大捐款金额是500元 |