在某次测试后,班里有两位同学议论他们小组的数学成绩,小明说:“我们组考87分的人最多”,小华说:“我们组7位同学成绩排在最中间的恰好也是87分”.上面两位同学的话能反映出的统计量是
A.众数和平均数B.平均数和中位数
C.众数和方差D.众数和中位数
如表是某公司员工月收入的资料.
月收入 元 |
45000 |
18000 |
10000 |
5500 |
5000 |
3400 |
3300 |
1000 |
人数 |
1 |
1 |
1 |
3 |
6 |
1 |
11 |
1 |
能够反映该公司全体员工月收入水平的统计量是
A.平均数和众数B.平均数和中位数
C.中位数和众数D.平均数和方差
某班要从9名百米跑成绩各不相同的同学中选4名参加 米接力赛,而这9名同学只知道自己的成绩,要想让他们知道自己是否入选,老师只需公布他们成绩的
A.平均数B.中位数C.众数D.方差
我们家乡的黑土地全国特有,肥沃的土壤、绿色的水源是优质大米得天独厚的生长条件,因此黑龙江的大米在全国受到广泛欢迎,小明在平价米店记录了一周中不同包装 , , 的大米的销售量(单位:袋)如下: 装100袋; 装220袋; 装80袋,如果每千克大米的进价和销售价都相同,则米店老板最应该关注的是这些数据(千克数)中的
A.众数B.平均数C.中位数D.方差
某商场试销售某品牌男款运动鞋,一个月内销售情况如下表:
型号 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
数量(件 |
5 |
7 |
12 |
15 |
23 |
25 |
14 |
商场经理要想了解哪种型号需求量最大,则上述数据的统计量中,对商场经理来说最有意义的是
A.平均数B.方差C.中位数D.众数
在某校“我的中国梦”演讲比赛中,有7名学生参加决赛,他们决赛的最终成绩各不相同,其中一名学生想要知道自己能否进入前3名,他不仅要了解自己的成绩,还要了解这7名学生成绩的
A.众数B.方差C.平均数D.中位数
在“我的阅读生活”校园演讲比赛中,有11名学生参加比赛,他们决赛的最终成绩各不相同,其中一名学生想知道自己能否进入前6名,除了要了解自己的成绩外,还要了解这11名学生成绩的
A.众数B.方差C.平均数D.中位数
有五名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的
A.方差B.中位数C.众数D.平均数
某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
尺码 |
39 |
40 |
41 |
42 |
43 |
平均每天销售数量 件 |
10 |
12 |
20 |
12 |
12 |
该店主决定本周进货时,增加了一些41码的衬衫,影响该店主决策的统计量是
A.平均数B.方差C.众数D.中位数
某校有35名同学参加眉山市的三苏文化知识竞赛,预赛分数各不相同,取前18名同学参加决赛.其中一名同学知道自己的分数后,要判断自己能否进入决赛,只需要知道这35名同学分数的
A.众数B.中位数C.平均数D.方差
某鞋厂调查了商场一个月内不同尺码男鞋的销量,在平均数、中位数、众数和方差等数个统计量中,该鞋厂最关注的是 .
九年级两名男同学在体育课上各练习10次立定跳远,平均成绩均为2.20米,要判断哪一名同学的成绩比较稳定,通常需要比较这两名同学立定跳远成绩的
A.方差B.众数C.平均数D.中位数
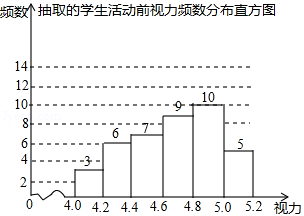
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到 ;活动后,再次检查这部分学生的视力,结果如表所示.
分组 |
频数 |
|
2 |
|
3 |
|
5 |
|
8 |
|
17 |
|
5 |
(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.
为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如图所示.

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 |
3首 |
4首 |
5首 |
6首 |
7首 |
8首 |
人数 |
10 |
10 |
15 |
40 |
25 |
20 |
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.