初中数学频数（率）分布表试题

某校为了解九年级学生每天参加体育锻炼的时间，从该校九年级学生中随机抽取20名学生进行调查，得到如下数据（单位：分钟） $:$

306070103011570607590157040751058060307045

对以上数据进行整理分析，得到下列表一和表二：

表一

时间 $t$（单位：分钟）	$0⩽t<30$	$30⩽t<60$	$60⩽t<90$	$90⩽t<120$
人数	2	$a$	10	$b$

表二

平均数	中位数	众数
60	$c$	$d$

根据以上提供的信息，解答下列问题：

（1）填空

① $a=$　    　， $b=$　    　；

② $c=$　   　， $d=$　    　；

（2）如果该校现有九年级学生200名，请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数．

某中学1000名学生参加了”环保知识竞赛“，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取整数，满分为100分）作为样本进行统计，并制作了如图频数分布表和频数分布直方图（不完整且局部污损，其中“■”表示被污损的数据）．请解答下列问题：

成绩分组	频数	频率
$50⩽x<60$	8	0.16
$60⩽x<70$	12	$a$
$70⩽x<80$	■	0.5
$80⩽x<90$	3	0.06
$90⩽x⩽100$	$b$	$c$
合计	■	1

（1）写出 $a$， $b$， $c$的值；

（2）请估计这1000名学生中有多少人的竞赛成绩不低于70分；

（3）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取两名同学参加环保知识宣传活动，求所抽取的2名同学来自同一组的概率．

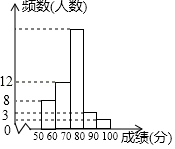
现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整） $:$

步数	频数	频率
$0⩽x<4000$	8	$a$
$4000⩽x<8000$	15	0.3
$8000⩽x<12000$	12	$b$
$12000⩽x<16000$	$c$	0.2
$16000⩽x<20000$	3	0.06
$20000⩽x<24000$	$d$	0.04

请根据以上信息，解答下列问题：

（1）写出 $a$， $b$， $c$， $d$的值并补全频数分布直方图；

（2）本市约有37800名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？

（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步）的两名教师与大家分享心得，求被选取的两名教师恰好都在20000步（包含20000步）以上的概率．

阅读对学生的成长有着深远的影响，某中学为了解学生每周课余阅读的时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表．

组别	时间（小时）	频数（人数）	频率
$A$	$0⩽t⩽0.5$	6	0.15
$B$	$0.5⩽t⩽1$	$a$	0.3
$C$	$1⩽t⩽1.5$	10	0.25
$D$	$1.5⩽t⩽2$	8	$b$
$E$	$2⩽t⩽2.5$	4	0.1
合计			1

请根据图表中的信息，解答下列问题：

（1）表中的 $a=$　        　， $b=$　       　，中位数落在　     　组，将频数分布直方图补全；

（2）估计该校2000名学生中，每周课余阅读时间不足0.5小时的学生大约有多少名？

（3） $E$组的4人中，有1名男生和3名女生，该校计划在 $E$组学生中随机选出两人向全校同学作读书心得报告，请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率．

某校为了解七年级学生的体重情况，随机抽取了七年级 $m$名学生进行调查，将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图．

组别	体重（千克）	人数
$A$	$37.5⩽x<42.5$	10
$B$	$42.5⩽x<47.5$	$n$
$C$	$47.5⩽x<52.5$	40
$D$	$52.5⩽x<57.5$	20
$E$	$57.5⩽x<62.5$	10

请根据图表信息回答下列问题：

（1）填空：

① $m=$　　，

② $n=$　　，

③在扇形统计图中， $C$组所在扇形的圆心角的度数等于　　度；

（2）若把每组中各个体重值用这组数据的中间值代替（例如： $A$组数据中间值为40千克），则被调查学生的平均体重是多少千克？

（3）如果该校七年级有1000名学生，请估算七年级体重低于47.5千克的学生大约有多少人？

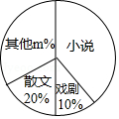
九年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”“戏剧”“散文”“其他”四个选项，每位同学仅选一项，根据调查结果绘制了如下不完整的频数分布表和扇形统计图．

类别	频数（人数）	频率
小说	16
戏剧	4
散文	$a$
其他	$b$
合计		1

根据图表提供的信息，解答下列问题：

（1）直接写出 $a$， $b$， $m$的值；

（2）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组，请用列表法或画树状图的方法，求选取的2人恰好是乙和丙的概率．

电子政务、数字经济、智慧社会 $\dots$一场数字革命正在神州大地激荡．在第二届数字中国建设峰会召开之际，某校举行了第二届“掌握新技术，走进数时代”信息技术应用大赛，将该校八年级参加竞赛的学生成绩统计后，绘制成如下统计图表（不完整） $:$

“掌握新技术，走进数时代”信息技术应用大赛成绩频数分布统计表

组别	成绩 $x$（分 $)$	人数
$A$	$60⩽x<70$	10
$B$	$70⩽x<80$	$m$
$C$	$80⩽x<90$	16
$D$	$90⩽x⩽100$	4

请观察上面的图表，解答下列问题：

（1）统计表中 $m=$　　；统计图中 $n=$　　， $D$组的圆心角是　　度．

（2） $D$组的4名学生中，有2名男生和2名女生．从 $D$组随机抽取2名学生参加 $5G$体验活动，请你画出树状图或用列表法求：

①恰好1名男生和1名女生被抽取参加 $5G$体验活动的概率；

②至少1名女生被抽取参加 $5G$体验活动的概率．

某中学为了了解学生每周在校体育锻炼时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表，请根据图表信息解答下列问题：

时间（小时）	频数（人数）	频率
$2⩽t<3$	4	0.1
$3⩽t<4$	10	0.25
$4⩽t<5$	$a$	0.15
$5⩽t<6$	8	$b$
$6⩽t<7$	12	0.3
合计	40	1

（1）表中的 $a=$　　， $b=$　　；

（2）请将频数分布直方图补全；

（3）若该校共有1200名学生，试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名？

甲、乙两城市某月1日 $~10$日中午12时的气温（单位： ${}^{°}\text{C})$如下：

甲 22 20 25 22 18 23 13 27 27 22

乙 21 22 24 18 28 21 18 19 26 18

整理数据：这两组数据的频数分布表如表一．

分析数据：这两组数据的平均数、中位数、众数和方差如表二所示．

表一

分组	频数
	甲	乙
$10⩽x<15$	1	0
$15⩽x<20$	1	$a$
$20⩽x<25$	5	$b$
$25⩽x<30$	3	2

表二

统计量	甲	乙
平均数	$c$	21.5
中位数	22	$d$
众数	22	$e$
方差	16.09	11.25

请填空：

（1）在上表中， $a=$　　， $b=$　　， $c=$　　， $d=$　　， $e=$　　；

（2）　　城的气温变化较小；

（3）　　城的气温较高，理由是　　．

某校为了解高一年级住校生在校期间的月生活支出情况，从高一年级600名住校学生中随机抽取部分学生，对他们今年4月份的生活支出情况进行调查统计，并绘制成如下统计图表：

组别	月生活支出 $x$（单位：元）	频数（人数）	频率
第一组	$x<300$	4	0.10
第二组	$300⩽x<350$	2	0.05
第三组	$350⩽x<400$	16	$n$
第四组	$400⩽x<450$	$m$	0.30
第五组	$450⩽x<500$	4	0.10
第六组	$x⩾500$	2	0.05

请根据图表中所给的信息，解答下列问题：

（1）在这次调查中共随机抽取了　　名学生，图表中的 $m=$　　， $n$　　；

（2）请估计该校高一年级600名住校学生今年4月份生活支出低于350元的学生人数；

（3）现有一些爱心人士有意愿资助该校家庭困难的学生，学校在本次调查的基础上，经过进一步核实，确认高一（2）班有 $A$， $B$， $C$三名学生家庭困难，其中 $A$， $B$为女生， $C$为男生．李阿姨申请资助他们中的两名，于是学校让李阿姨从 $A$， $B$， $C$三名学生中依次随机抽取两名学生进行资助，请用列表法（或树状图法）求恰好抽到 $A$， $B$两名女生的概率．

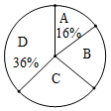
某市将开展以“走进中国数学史”为主题的知识竞赛活动，红树林学校对本校100名参加选拔赛的同学的成绩按 $A$， $B$， $C$， $D$四个等级进行统计，绘制成如下不完整的统计表和扇形统计图：

成绩等级	频数（人数）	频率
$A$	4	0.04
$B$	$m$	0.51
$C$	$n$
$D$
合计	100	1

（1）求 $m=$　　， $n=$　　；

（2）在扇形统计图中，求“ $C$等级”所对应圆心角的度数；

（3）成绩等级为 $A$的4名同学中有1名男生和3名女生，现从中随机挑选2名同学代表学校参加全市比赛，请用树状图法或者列表法求出恰好选中“1男1女”的概率．

某批彩色弹力球的质量检验结果如下表：

抽取的彩色弹力球数 $n$	500	1000	1500	2000	2500
优等品频数 $m$	471	946	1426	1898	2370
优等品频率 $\frac{m}{n}$	0.942	0.946	0.951	0.949	0.948

（1）请在图中完成这批彩色弹力球“优等品”频率的折线统计图

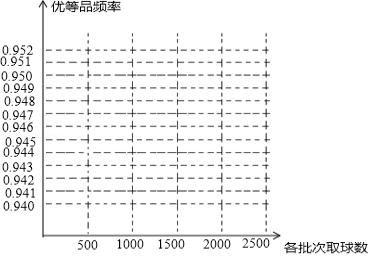
（2）这批彩色弹力球“优等品”概率的估计值大约是多少？（精确到0.01）

（3）从这批彩色弹力球中选择5个黄球、13个黑球、22个红球，它们除了颜色外都相同，将它们放入一个不透明的袋子中，求从袋子中摸出一个球是黄球的概率．

（4）现从第（3）问所说的袋子中取出若干个黑球，并放入相同数量的黄球，搅拌均匀，使从袋子中摸出一个黄球的概率为 $\frac{1}{4}$，求取出了多少个黑球？

为宣传6月8日世界海洋日，某校九年级举行了主题为"珍惜海洋资源，保护海洋生物多样性"的知识竞赛活动．为了解全年级500名学生此次竞赛成绩（百分制）的情况，随机抽取了部分参赛学生的成绩，整理并绘制出如下不完整的统计表（表1）和统计图（如图）．请根据图表信息解答以下问题：

（1）本次调查一共随机抽取了 　        　个参赛学生的成绩；

（2）表1中 $a=$ 　         　；

（3）所抽取的参赛学生的成绩的中位数落在的"组别"是 　            　；

（4）请你估计，该校九年级竞赛成绩达到80分以上（含80分）的学生约有 　           　人．

表1知识竞赛成绩分组统计表

组别	分数 $/$ 分	频数
$A$	$60⩽x<70$	$a$
$B$	$70⩽x<80$	10
$C$	$80⩽x<90$	14
$D$	$90⩽x<100$	18

在太空种子种植体验实践活动中，为了解"宇番2号"番茄，某校科技小组随机调查60株番茄的挂果数量 $x$ （单位：个），并绘制如下不完整的统计图表：

"宇番2号"番茄挂果数量统计表

挂果数量     $x$ （个）	频数（株）	频率
$25⩽x<35$	6	0.1
$35⩽x<45$	12	0.2
$45⩽x<55$	$a$	0.25
$55⩽x<65$	18	$b$
$65⩽x<75$	9	0.15

请结合图表中的信息解答下列问题：

（1）统计表中， $a=$ 　      　， $b=$ 　      　；

（2）将频数分布直方图补充完整；

（3）若绘制"番茄挂果数量扇形统计图"，则挂果数量在" $35⩽x<45$ "所对应扇形的圆心角度数为 　     　 $°$ ；

（4）若所种植的"宇番2号"番茄有1000株，则可以估计挂果数量在" $55⩽x<65$ "范围的番茄有 　      　株．

某地某月 $1~20$日中午12时的气温（单位： ${}^{°}\text{C})$如下：

22 31 25 15 18 23 21 20 27 17

20 12 18 21 21 16 20 24 26 19

（1）将下列频数分布表补充完整：

气温分组	划记	频数
$12⩽x<17$		3
$17⩽x<22$
$22⩽x<27$
$27⩽x<32$		2

（2）补全频数分布直方图；

（3）根据频数分布表或频数分布直方图，分析数据的分布情况．