某地某月 日中午12时的气温（单位： 如下：
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19
（1）将下列频数分布表补充完整：
气温分组 |
划记 |
频数 |
|
|
3 |
|
|
|
|
|
|
|
|
2 |
（2）补全频数分布直方图；
（3）根据频数分布表或频数分布直方图，分析数据的分布情况．
相关试题
如图，反比例函数
（k为常数，且k≠0）经过点A（1，3）．
（1）求反比例函数的解析式；
（2）在x轴正半轴上有一点B，若△AOB的面积为6，求直线AB的解析式．
如图，在平面直角坐标系中，双曲线
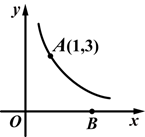
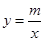和直线y＝kx＋b交于A，B两点，点A的坐标为（－3，2），BC⊥y轴于点C，且OC＝6BC．
（1）求双曲线和直线的解析式；
（2）直接写出不等式
的解集．
已知A（0，－6），B（－3，0），C（m，2）三点在同一直线上，试求出图象经过其中一点的反比例函数的解析式，并在图中画出其图象．（要求标出必要的点，可不写画法）
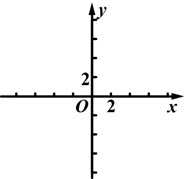
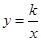(k≠0)的图象经过点(
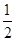，8)，直线y＝－x＋b经过反比例函数图象上的点Q(4，m)，求反比例函数和直线的解析式．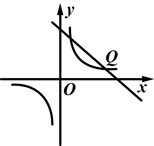
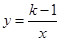（k为常数，k≠1）．相关知识点
推荐套卷
粤公网安备 44130202000953号