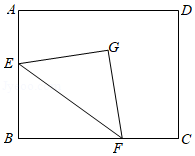
如图,在矩形 中, , ,点 , 分别是边 , 上的动点,点 不与 , 重合,且 , 是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点 到边 , 的距离一定相等;
③点 到边 , 的距离可能相等;
④点 到边 的距离的最大值为 .
其中正确的是 .(写出所有正确结论的序号)
如图,在 中, , , ,点 在边 上, ,联结 .如果将 沿直线 翻折后,点 的对应点为点 ,那么点 到直线 的距离为 .

如图,抛物线与
轴交于点
,点
,与
轴交于点
,且过点
.点
、
是抛物线
上的动点.
(1)求抛物线的解析式;
(2)当点在直线
下方时,求
面积的最大值.
(3)直线与线段
相交于点
,当
与
相似时,求点
的坐标.

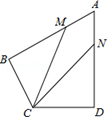
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2.则∠BCD= °,cos∠MCN= .
某校数学兴趣小组要测量西山植物园蒲宁之珠的高度.如图,他们在点A处测得蒲宁之珠最高点C的仰角为45°,再往蒲宁之珠方向前进至点B处测得最高点C的仰角为56°,AB=62m,根据这个兴趣小组测得的数据,则蒲宁之珠的高度CD约为 m.(sin56°≈0.83,tan56°≈1.49,结果保留整数)
如图1为两个边长为1的正方形组成的 格点图,点A,B,C,D都在格点上,AB,CD交于点P,则tan∠BPD= ,如果是n个边长为1的正方形组成的
格点图,点A,B,C,D都在格点上,AB,CD交于点P,则tan∠BPD= ,如果是n个边长为1的正方形组成的 格点图,如图2,那么tan∠BPD= .
格点图,如图2,那么tan∠BPD= .
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN= 
如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果 ,
, .那么m与n满足的关系式是:m= (用含n的代数式表示m).
.那么m与n满足的关系式是:m= (用含n的代数式表示m).
如图,半径为6cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连结AE,BF,则图中两个阴影部分的面积为 cm2
如图,所有正三角形的一边平行于x轴,一顶点在y轴上.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用 表示,其中x轴与边
表示,其中x轴与边 ,边
,边 与
与 ,
, 与
与 ,…均相距一个单位,则顶点
,…均相距一个单位,则顶点 的坐标为 ;
的坐标为 ; 的坐标为 ;
的坐标为 ; (n为正整数)的坐标为 .
(n为正整数)的坐标为 .
在平面直角坐标系 中,点
中,点 ,
, ,
, ,…和
,…和 ,
, ,
, ,…分别在直线
,…分别在直线 和
和 轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(
轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2( ),那么点
),那么点 的纵坐标是_ _____.
的纵坐标是_ _____.