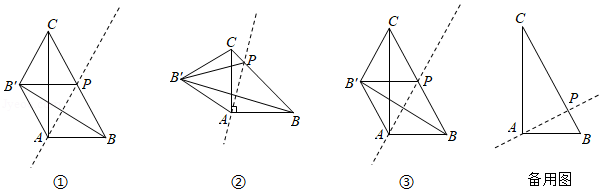
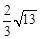在等边 中, , ,垂足为 ,点 为 边上一点,点 为直线 上一点,连接 .
(1)将线段 绕点 逆时针旋转 得到线段 ,连接 .
①如图1,当点 与点 重合,且 的延长线过点 时,连接 ,求线段 的长;
②如图2,点 不与点 , 重合, 的延长线交 边于点 ,连接 ,求证: ;
(2)如图3,当点 为 中点时,点 为 中点,点 在边 上,且 ,点 从 中点 沿射线 运动,将线段 绕点 顺时针旋转 得到线段 ,连接 ,当 最小时,直接写出 的面积.
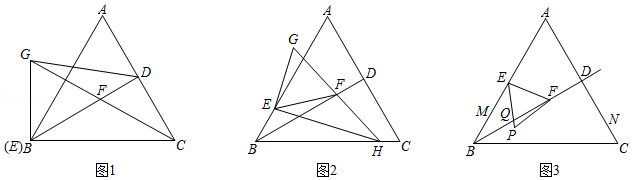
问题提出
(1)如图1,在 中, , , , 是 的中点,点 在 上,且 ,求四边形 的面积.(结果保留根号)
问题解决
(2)某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上规划一个五边形河畔公园 .按设计要求,要在五边形河畔公园 内挖一个四边形人工湖 ,使点 、 、 、 分别在边 、 、 、 上,且满足 , .已知五边形 中, , , , , .为满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖 ?若存在,求四边形 面积的最小值及这时点 到点 的距离;若不存在,请说明理由.
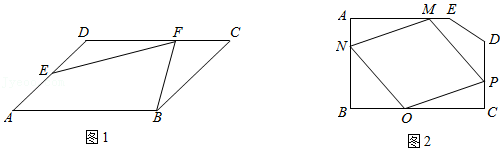
已知点 是线段 的中点,点 是直线 上的任意一点,分别过点 和点 作直线 的垂线,垂足分别为点 和点 .我们定义垂足与中点之间的距离为"足中距".
(1) 猜想验证 如图1,当点 与点 重合时,请你猜想、验证后直接写出"足中距" 和 的数量关系是 .
(2) 探究证明 如图2,当点 是线段 上的任意一点时,"足中距" 和 的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3) 拓展延伸 如图3,①当点 是线段 延长线上的任意一点时,"足中距" 和 的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若 ,请直接写出线段 、 、 之间的数量关系.
如图,在 中,点 为斜边 上一动点,将 沿直线 折叠,使得点 的对应点为 ,连接 , , , .
(1)如图①,若 ,证明: .
(2)如图②,若 , ,求 的值.
(3)如图③,若 ,是否存在点 ,使得 .若存在,求此时 的值;若不存在,请说明理由.
下面是某数学兴趣小组探究用不同方法作一个角的平分线的讨论片段,请仔细阅读,并完成相应的任务.
小明:如图1, 分别在射线OA,OB上截取 , 点C,E不重合 ; 分别作线段CE,DF的垂直平分线 , ,交点为P,垂足分别为点G,H; 作射线OP,射线即为 的平分线. 简述理由如下: 由作图知, , , ,所以 ≌ ,则 ,即射线OP是 的平分线. 小军:我认为小明的作图方法很有创意,但是太麻烦了,可以改进如下,如图2, 分别在射线OA,OB上截取 , 点C,E不重合 ; 连接DE,CF,交点为P; 作射线 射线OP即为 的平分线.
|
任务:

小明得出 ≌ 的依据是______ 填序号 .
小军作图得到的射线0P是 的平分线吗?请判断并说明理由.
如图3,已知 ,点E,F分别在射线OA,OB上,且 点C,D分别为射线OA,OB上的动点,且 ,连接DE,CF,交点为P,当 时,直接写出线段OC的长.
在一平面内,线段 ,线段 ,将这四条线段顺次首尾相接.把 固定,让 绕点 从 开始逆时针旋转角 到某一位置时, , 将会跟随出现到相应的位置.
论证:如图1,当 时,设 与 交于点 ,求证: ;
发现:当旋转角 时, 的度数可能是多少?
尝试:取线段 的中点 ,当点 与点 距离最大时,求点 到 的距离;
拓展:①如图2,设点 与 的距离为 ,若 的平分线所在直线交 于点 ,直接写出 的长(用含 的式子表示);
②当点 在 下方,且 与 垂直时,直接写出 的余弦值.

如图1,矩形ABCD中,AB=2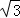 ,BC=6,点P、Q分别是线段AD和线段BC上的动点,满足∠PQB=60°.
,BC=6,点P、Q分别是线段AD和线段BC上的动点,满足∠PQB=60°.
(1)填空:①∠ACB= 度;②PQ= .
(2)设线段BC的中点为N,PQ与线段AC相交于点M,若△CMN为直角三角形,请直接写出满足条件的AP的长度.
(3)设AP=x,△PBQ与△ABC的重叠部分的面积为S,试求S与x的函数关系式和自变量x的取值范围.
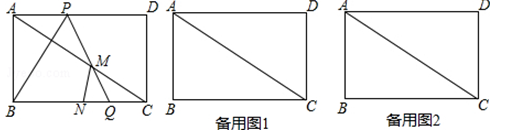
如图,二次函数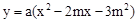 (其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a;
(2))求证: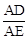 为定值;
为定值;
(3)设该二次函数图象的顶点为F.探索:在x轴的负半轴上是否存在点G,连接CF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.
如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2cm.矩形ABCD的边AD,AB分别与l1,l2重合,AB=4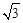 cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
(1)如图①,连接OA,AC,则∠OAC的度数为 °;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围.(解答时可以利用备用图画出相关示意图)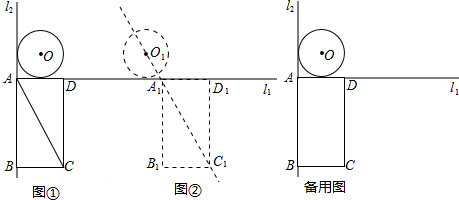
等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N(如图1)。
(1)求证:AM=AN;
(2)设BP=x。
①若,BM=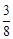 ,求x的值;
,求x的值;
②记四边形ADPE与△ABC重叠部分的面积为S,求S与x之间的函数关系式以及S的最小值;
③连接DE,分别与边AB、AC交于点G、H(如图2),当x取何值时,∠BAD=150?并判断此时以DG、GH、HE这三条线段为边构成的三角形是什么特殊三角形,请说明理由。
在平面直角坐标系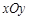 中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作
中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作 .
.
(1)已知⊙O是以原点为圆心,1为半径的圆,点P(0,2),
①直线 :
: ,直线
,直线 :
: ,直线
,直线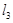 :
: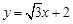 ,直线
,直线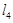 :
: 都经过点P,在直线
都经过点P,在直线 ,
,  ,
, 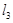 ,
, 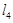 中,是⊙O的“x关联直线”的是 ;
中,是⊙O的“x关联直线”的是 ;
②若直线 是⊙O的“x关联直线”,则点M的横坐标
是⊙O的“x关联直线”,则点M的横坐标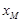 的最大值是 ;
的最大值是 ;
(2)点A(2,0),⊙A的半径为1,
①若P(-1,2),⊙A的“x关联直线” :
: ,点M的横坐标为
,点M的横坐标为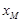 ,当
,当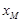 最大时,求k的值;
最大时,求k的值;
②若P是y轴上一个动点,且点P的纵坐标 ,⊙A的两条“x关联直线”
,⊙A的两条“x关联直线” ,
,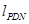 是⊙A的两条切线,切点分别为C,D,作直线CD与x轴点于点E,当点P的位置发生变化时, AE的长度是否发生改变?并说明理由.
是⊙A的两条切线,切点分别为C,D,作直线CD与x轴点于点E,当点P的位置发生变化时, AE的长度是否发生改变?并说明理由.
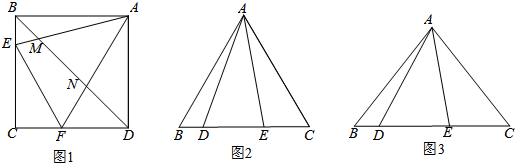
(1)如图1,点E、F分别是正方形ABCD的边BC、CD上的点,∠EAF=45°,连接EF,
则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足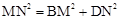 ,请证明这个等量关系;
,请证明这个等量关系;
(2)在△ABC中, AB=AC,点D、E分别为BC边上的两点.
①如图2,当∠BAC=60°,∠DAE=30°时,BD、DE、EC应满足的等量关系是__________________;
②如图3,当∠BAC= ,(0°<
,(0°< <90°),∠DAE=
<90°),∠DAE= 时,BD、DE、EC应满足的等量关系是____________________.【参考:
时,BD、DE、EC应满足的等量关系是____________________.【参考: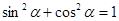 】
】
菱形ABCD的对角线AC,BD相交于点O, .动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为
.动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为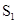 ,未盖住部分的面积为
,未盖住部分的面积为 ,
, .
.
(1)用含x代数式分别表示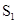 ,
, ;
;
(2)若 ,求x.
,求x.
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
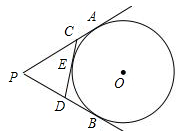
A.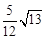 B.
B.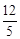 C.
C.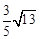 D.
D.