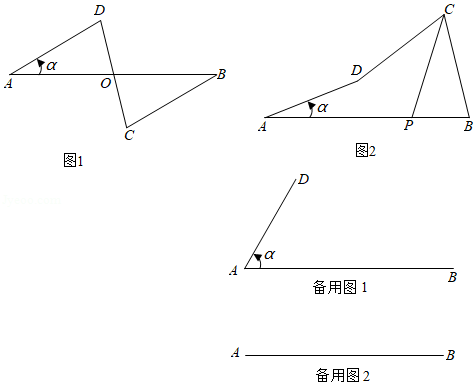
在一平面内,线段 ,线段 ,将这四条线段顺次首尾相接.把 固定,让 绕点 从 开始逆时针旋转角 到某一位置时, , 将会跟随出现到相应的位置.
论证:如图1,当 时,设 与 交于点 ,求证: ;
发现:当旋转角 时, 的度数可能是多少?
尝试:取线段 的中点 ,当点 与点 距离最大时,求点 到 的距离;
拓展:①如图2,设点 与 的距离为 ,若 的平分线所在直线交 于点 ,直接写出 的长(用含 的式子表示);
②当点 在 下方,且 与 垂直时,直接写出 的余弦值.
相关知识点
推荐套卷
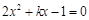
 米的点P处.这时,一辆出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为
米的点P处.这时,一辆出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为 秒且∠APO=60°,∠BPO =45°.
秒且∠APO=60°,∠BPO =45°. 
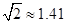 ,
,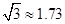 )
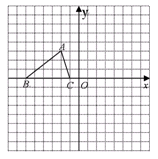
) 的三个顶点的坐标分别为
的三个顶点的坐标分别为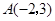 、
、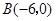 、
、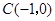 .
.
 关于
关于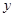 轴对称的点的坐标
轴对称的点的坐标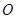 逆时针旋转90°.画出图形,直接写出点
逆时针旋转90°.画出图形,直接写出点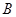 的对应点的坐标
的对应点的坐标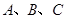 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点 的坐标.
的坐标.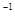 -tan60°+(
-tan60°+(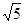 -1)
-1)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号