初中数学解直角三角形试题

如图，为了测量楼的高度，自楼的顶部A看地面上的一点B，俯角为30°，已知地面上的这点与楼的水平距离BC为30m，那么楼的高度AC为        m（结果保留根号）．

如图，方格纸中有三个格点A．B．C，则sin∠ABC=          ．

以下列长度（单位：cm）为边长的三角形是直角三角形的是（  ）

A．5，6，7

B．7，8，9

C．6，8，10

D．5，7，9

如图，在四边形ABCD中，E、F分別是AB、AD的中点，若EF=2，BC=5，CD=3，则tanC等于（ ）

A、        B、          C、          D、

计算：．

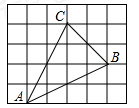
如图，在正方形网格中，小正方形的边长均为1，点A、B、C都是格点，则cos∠BAC=     ．

2cos30°−=     ．

如图，河坝横断面迎水坡AB的坡比为1：（坡比是坡面的铅直高度BC与水平宽度AC之比），坝高BC=3m，则坡面AB的长度是                m．

的值等于（     ）

A．

B．

C．

D．

在锐角△ABC中，|sinA-|+（cosB－）²="0" ，则∠C的度数是（  ）

A．30°

B．45°

C．60°

D．75°

如图，由边长为1的小正方形组成的网格中， A、B、C三点都在网格的格点上．则tan∠BAC=           ．

如图，AB是⊙O的直径，弦BC=2cm，∠ABC=60°．若动点P以2cm/s的速度从B点出发沿着B→A的方向运动，点Q以1cm/s的速度从A点出发沿着A→C的方向运动，当点P到达点A时，点Q也随之停止运动．设运动时间为t（s），当△APQ是直角三角形时，t的值为         ．

如图，在地面上的点A处测得树顶B的仰角α=75º， 若AC＝6米，则树高BC为 （ ）

A．6sin75º米

B．米

C．米

D．6tan75º米

如图1是小志同学书桌上的一个电子相框，将其侧面抽象为如图2所示的几何图形，已知BC=BD=15cm，∠CBD=40°，则点B到CD的距离为       cm（参考数据：sin20°≈0．342，cos20°≈0．940，sin40°≈0．643，cos40°≈0．766．计算结果精确到0．1cm，可用科学计算器）．

如图，网格中的每个小正方形的边长都是1，△ABC每个顶点都在网格的交点处，则sinA=       ．