如图,是
的直径,点
为
上一点,
于点
,交
于点
,点
为
的延长线上一点,
的延长线与
的延长线交于点
,且
,连结
、
、
.
(1)求证:为
的切线;
(2)过作
于点
,求证:
;
(3)如果,
,求
的长.

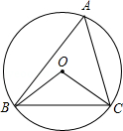
如图, 的半径为4, 是 的内接三角形,连接 、 .若 与 互补,则弦 的长为
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形 中, , , 是 的中点,将 沿 折叠,点 落在矩形内点 处,连接 ,则 .

如图, 经过平面直角坐标系的原点 ,交 轴于点 ,交 轴于点 ,点 为第二象限内圆上一点.则 的正弦值是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,为
的直径,
为
上的一点,
,
,
的延长线交
于点
,连接
.
(1)求证:是
的切线;
(2)若为
的中点,求
的值.
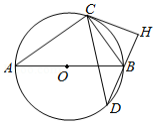
如图,在 中, , , 、 分别在 、 上,点 在 内.若四边形 是边长为1的正方形,则 .

如图,在平面直角坐标系中,菱形 的边 在 轴上,点 , .若反比例函数 经过点 ,则 的值等于

| A. |
10 |
B. |
24 |
C. |
48 |
D. |
50 |
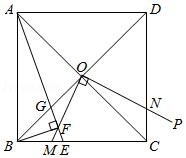
如图,在正方形 中,对角线 , 相交于点 ,点 在 边上,且 ,连接 交 于点 ,过点 作 于点 ,连接 并延长,交 于点 ,过点 作 交 于点 , ,现给出下列结论:① ;② ;③ ;④ ;其中正确的结论有
| A. |
①②③ |
B. |
②③④ |
C. |
①②④ |
D. |
①③④ |
如图,定义:在 中,
中, ,锐角
,锐角 的邻边与对边的比叫做角
的邻边与对边的比叫做角 的余切,记作
的余切,记作 ,即
,即 =
= .
.

根据上述角的余切定义,解答下列问题:
(1) = .
= .
(2)求 的值.
的值.
如图,根据图中数据解答下列问题.
(1)sin2A1+sin2B1=________;
sin2A2+sin2B2=________;
sin2A3+sin2B3=________.
观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B=________.
(2)如图④,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理,证明(1)中的猜想.
(3)已知∠A+∠B=90°,且 ,求sinB.
,求sinB.
如图,在 中, , , ,以 的中点 为圆心, 的长为半径作半圆交 于点 ,则图中阴影部分的面积为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , 和 关于直线 对称,连接 ,与 相交于点 ,过点 作 ,垂足为 , 相交于点 ,若 , ,则 的值为

A. B. C. D.
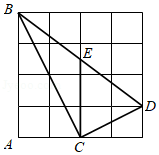
如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是
| A. |
|
B. |
|
C. |
|
D. |
|