如图,矩形 的对角线 、 相交于点 , ,且 , ,连接 ,则

A. B. C. D.
如图,在菱形纸片 中, , ,将菱形纸片翻折,使点 落在 的中点 处,折痕为 ,点 , 分别在边 , 上,则 的值为 .
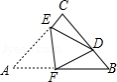
如图,在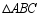 中,
中,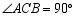 ,
,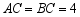 ,将
,将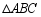 折叠,使点
折叠,使点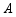 落在
落在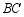 边上的点
边上的点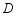 处,
处,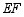 为折痕,若
为折痕,若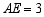 ,则
,则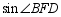 的值为
的值为
A. B. C. D.
如图,矩形 中,点 , 分别在边 , 上,连接 , , ,将 和 分别沿 , 折叠,使点 , 恰好落在 上的同一点,记为点 .若 , ,则 .

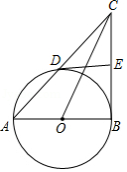
如图,线段  是
是 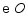 的直径,弦
的直径,弦 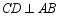 于点
于点 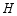 ,点
,点 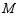 是
是 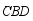 上任意一点,
上任意一点, 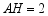 ,
, 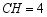 .
.
(1)求 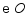 的半径
的半径 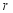 的长度;
的长度;
(2)求 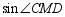 ;
;
(3)直线 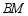 交直线
交直线 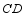 于点
于点 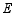 ,直线
,直线 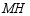 交
交 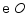 于点
于点 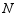 ,连接
,连接 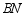 交
交 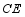 于点
于点 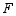 ,求
,求 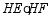 的值.
的值.
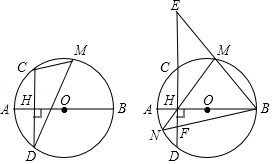
如图,在矩形 中, , ,点 在 上,将矩形 沿 折叠,点 恰好落在 边上的点 处,那么 的值是 .
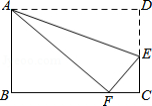
如图,在 的正方形网格图中,已知点 、 、 、 、 均在格点上,其中 、 、 又在 上,点 是线段 与 的交点.则 的正切值为 .
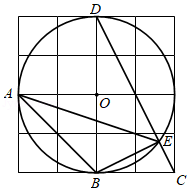
如图,在 中, , 和 关于直线 对称,连接 ,与 相交于点 ,过点 作 ,垂足为 , 相交于点 ,若 , ,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
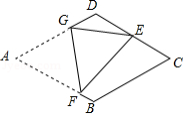
如图,在菱形 中,对角线 与 相交于点 , , ,点 在边 上, ,连结 交 于点 .
(1)求 的长.
(2) 的值为 .

问题探究:
小红遇到这样一个问题:如图1, 中, , , 是中线,求 的取值范围.她的做法是:延长 到 ,使 ,连接 ,证明 ,经过推理和计算使问题得到解决.
请回答:(1)小红证明 的判定定理是: ;
(2) 的取值范围是 ;
方法运用:
(3)如图2, 是 的中线,在 上取一点 ,连结 并延长交 于点 ,使 ,求证: .
(4)如图3,在矩形 中, ,在 上取一点 ,以 为斜边作 ,且 ,点 是 的中点,连接 , ,求证: .

如图, 是 的直径,点 在 上(点 不与 , 重合),直线 交过点 的切线于点 ,过点 作 的切线 交 于点 .
(1)求证: ;
(2)若 ,求 的值.