如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F, ,垂足为点E, ,垂足为点G,点H在边BC上, ,连接AH、FH,FH与AC交于点M,以下结论:
① ;② ;③ ;④ ;⑤ ,
其中正确结论的个数为( )

A.2B.3C.4D.5
如图, 为 的直径,弦 于点 , 于点 ,若 , ,则 的长度是
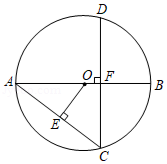
| A. |
9.6 |
B. |
|
C. |
|
D. |
10 |
如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是 ,则矩形ABCD的面积是( )
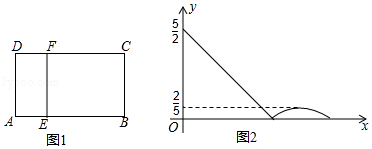
A. B.5C.6D.
如图,在正方形 中, ,点 在 的边上,且 , 与 关于 所在的直线对称,将 按顺时针方向绕点 旋转 得到 ,连接 ,则线段 的长为

A.3B. C. D.
如图,▱ ABCD中, AB=2, AD=4,对角线 AC, BD相交于点 O,且 E, F, G, H分别是 AO, BO, CO, DO的中点,则下列说法正确的是( )
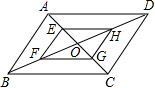
| A. |
EH=HG |
| B. |
四边形EFGH是平行四边形 |
| C. |
AC⊥BD |
| D. |
△ABO的面积是△EFO的面积的2倍 |
如图,在 中,点 、 分别是 、 的中点,若 的面积为4,则 的面积为

A.8B.12C.14D.16
如图, D、 E分别是△ ABC边 AB, AC上的点,∠ ADE=∠ ACB,若 AD=2, AB=6, AC=4,则 AE的长是( )

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
如图示,若 内一点 满足 ,则点 为 的布洛卡点.三角形的布洛卡点 是法国数学家和数学教育家克洛尔 . . 于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡 重新发现,并用他的名字命名.问题:已知在等腰直角三角形 中, ,若点 为 的布洛卡点, ,则
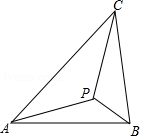
A.5B.4C. D.
如图,在四边形 ABCD中, BD平分∠ ABC,∠ BAD=∠ BDC=90°, E为 BC的中点, AE与 BD相交于点 F.若 BC=4,∠ CBD=30°,则 DF的长为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,点 A(﹣2,0), B(0,1),以线段 AB为边在第二象限作矩形 ABCD,双曲线 y= 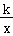 ( k<0)过点 D,连接 BD,若四边形 OADB的面积为6,则 k的值是( )
( k<0)过点 D,连接 BD,若四边形 OADB的面积为6,则 k的值是( )
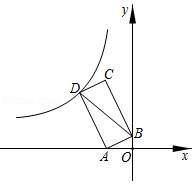
A.﹣9B.﹣12C.﹣16D.﹣18
如图,在平行四边形 中,点 在边 上, ,连接 交 于点 ,则 的面积与 的面积之比为

A. B. C. D.
如图,在正方形 中, , 是 边上的一点, 。将 沿 对折至 ,连接 ,则 的长是
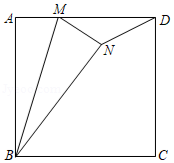
| A. |
|
B. |
|
C. |
3 |
D. |
|
如图, 的顶点 , ,点 在 轴的正半轴上,延长 交 轴于点 .将 绕点 顺时针旋转得到△ ,当点 的对应点 落在 上时, 的延长线恰好经过点 ,则点 的坐标为

| A. |
, |
B. |
, |
C. |
, |
D. |
, |
如图,在 中, , 分别与 , 相交于点 , ,若 , ,则 的值为

A. B. C. D.