如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若 ,AE=4,求CD.

如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.

如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)

如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D,E为 的中点,连接CE,BE,BE交AC于F.
(1)求证:AB=AF;
(2)若AB=3,BC=4,求CE的长.

如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH= .

如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为 .
如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°;②S▱ABCD=AC•BC;③OE:AC= :6;④S△OCF=2S△OEF
:6;④S△OCF=2S△OEF
成立的个数有( )

A.1个B.2个C.3个D.4个
如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.

如图,⊙ O是△ ABC的外接圆, BC是⊙ O的直径,∠ ABC=30°,过点 B作⊙ O的切线 BD,与 CA的延长线交于点 D,与半径 AO的延长线交于点 E,过点 A作⊙ O的切线 AF,与直径 BC的延长线交于点 F.
(1)求证:△ ACF∽△ DAE;
(2)若 ,求 DE的长;
(3)连接 EF,求证: EF是⊙ O的切线.

如图,已知⊙ O的半径为2, AB为直径, CD为弦. AB与 CD交于点 M,将 沿 CD翻折后,点 A与圆心 O重合,延长 OA至 P,使 AP= OA,连接 PC
(1)求 CD的长;
(2)求证: PC是⊙ O的切线;
(3)点 G为 的中点,在 PC延长线上有一动点 Q,连接 QG交 AB于点 E.交 于点 F( F与 B、 C不重合).问 GE• GF是否为定值?如果是,求出该定值;如果不是,请说明理由.

如图, CB= CA,∠ ACB=90°,点 D在边 BC上(与 B、 C不重合),四边形 ADEF为正方形,过点 F作 FG⊥ CA,交 CA的延长线于点 G,连接 FB,交 DE于点 Q,给出以下结论:
① AC= FG;② S △ FAB: S 四边形 CBFG=1:2;③∠ ABC=∠ ABF;④ AD 2= FQ• AC,
其中正确的结论的个数是( )

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
如图,在平面直角坐标系 xOy中,直线 y=﹣ x+3与 x轴交于点 C,与直线 AD交于点 ,点 D的坐标为(0,1)
(1)求直线 AD的解析式;
(2)直线 AD与 x轴交于点 B,若点 E是直线 AD上一动点(不与点 B重合),当△ BOD与△ BCE相似时,求点 E的坐标.

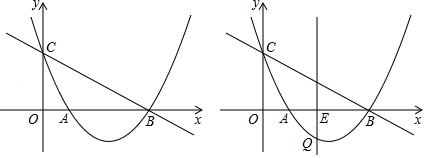
如图,已知二次函数 的图象与 轴交于 , 两点,与 轴交于点 ,直线 经过 , 两点.
(1)直接写出二次函数的解析式 ;
(2)平移直线 ,当直线 与抛物线有唯一公共点 时,求此时点 的坐标;
(3)过(2)中的点 作 轴,交 轴于点 .若点 是抛物线上一个动点,点 是 轴上一个动点,是否存在以 , , 三点为顶点的直角三角形(其中 为直角顶点)与 相似?如果存在,请直接写出满足条件的点 的个数和其中一个符合条件的点 的坐标;如果不存在,请说明理由.
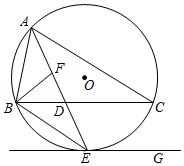
如图, 是 的外接圆,直线 与 相切于点 , ,连接 交 于点 .
(1)求证: 平分 ;
(2)若 的平分线 交 于点 ,且 , ,求 的长.