下列各种图形相似的是 ( )
A.(1)、(2) |
B.(3)、(4) | C.(1)、(3) | D.(1)、(4) |
如图,在直角坐标系中△ABC的A、B、C三点坐标为A(7,1)、B(8,2)、C(9,0).
(1) 请在图中画出△ABC的以点P (12,0)为位似中心,且与△ABC的相似比为3的位似图形△A/B/C/(要求与△ABC同在P点一侧);
(2)求线段BC的对应线段 所在直线的解析式.
所在直线的解析式.
如图,点C、D在线段AB上,△PCD是等边三角形.
(1)当AC、CD、DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是4,9和49.则△ABC的面积是 .
如图,已知△ABC 三个顶点的坐标分别为(1,2),(-2,3),(-1,0)。把它们的横坐标和纵坐标分别变成原来的2倍,得到点A、B、C,下列说法正确的是( )
A. △A/B/C/和△ABC是位似图形,位似中心是(1,0)。
B.△A/B/C/和△ABC是位似图形,位似中心是(0,0)。
C. △A/B/C/和△ABC是相似图形,但不是位似图形。
D.△A/B/C/和△ABC不是相似图形.
在比例尺为1∶20000的地图上,相距3cm的A、B两地的实际距离是____
如图所示,矩形ABCD中,AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、MN、FN,过ΔFMN三边的中点作ΔPQW.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题: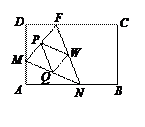
(1)说明ΔFMN∽ΔQWP;
(2)设0≤x≤4.试问x为何值时,ΔPQW为直角三角形?
(3)试用含的代数式表示MN2,并求当x为何值时,MN2最小?求此时MN2的值.
如图,路边有一根电线杆AB和一块半圆形广告牌,在太阳光照射下,杆顶A的影子刚好落在半圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在平地上一点E,若BC=5米,半圆形的广告牌直径为6米,DE=2米.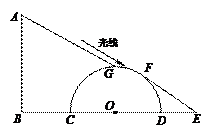
(1)求电线杆落在广告牌上的影子长(即︵CG的长).
(2)求电线杆的高度.
如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并说明你的理由;
(2)若AB=,BC=2,求⊙O的半径.
如图,已知∆ABC中,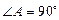 ,
, ,D是AB上一动点,DE∥BC,交AC于E,将四边形BDEC沿DE向上翻折,得四边形
,D是AB上一动点,DE∥BC,交AC于E,将四边形BDEC沿DE向上翻折,得四边形 ,
,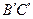 与AB、AC分别交于点M、N.
与AB、AC分别交于点M、N.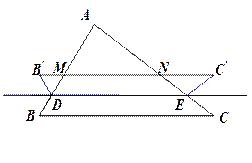
(1)证明:∆ADE 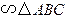 ;
;
(2)设AD为x,梯形MDEN的面积为y,试求y与x的函数关系式. 当x为何值时y有最大值?
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D.则△BCD与△ABC的周长之比为( )
A.1︰2 B.1︰3 C.1︰4 D.1︰5
AB是⊙O的直径,点E是半圆上一动点(点E与点A、B都不重合),点C是BE延长线上的一点,且CD⊥AB,垂足为D,CD与AE交于点H,点H与点A不重合。
(1)求证:△AHD∽△CBD
(2)连HB,若CD=AB=2,求HD+HO的值