2011届辽宁省凌海市初三上学期期末数学卷
某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量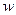 (千克)随销售单价
(千克)随销售单价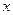 (元/千克)的变化而变化,具体关系式为:
(元/千克)的变化而变化,具体关系式为: ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为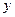 (元),解答下列问题:
(元),解答下列问题:
(1)求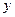 与
与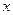 的关系式;
的关系式;
(2)当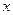 取何值时,
取何值时,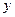 的值最大?
的值最大?
(3)如果公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
如图, 已知抛物线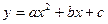 与x轴相交于A、B,点B的坐标为(10,0),顶点M的坐标为(4,8),点P从点M出发,以每秒1个单位的速度沿线段MA向A点运动;点Q从点A出发,以每秒2个单位的速度沿AB向B点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟。
与x轴相交于A、B,点B的坐标为(10,0),顶点M的坐标为(4,8),点P从点M出发,以每秒1个单位的速度沿线段MA向A点运动;点Q从点A出发,以每秒2个单位的速度沿AB向B点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟。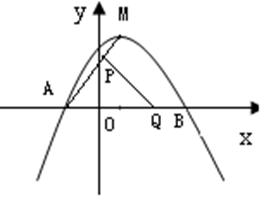
(1)求抛物线的解析式;
(2)设△APQ的面积为S,求S与t之间的函数关系式,△APQ的面积是否有最大值?若有,请求出其最大值;若没有,请说明理由;
(3)当t为何值时,△APQ为等腰三角形?
如图,△ABC中,∠ACB=90°, ∠A=30°AC的中垂线交AC于E.交AB于D,则图中60°的角共有 ( )
| A.6个 | B.5个 | C.4个 | D.3个 |
方程x2-2(3x-2)+(x+1)=0的一般形式是 ( )
| A.x2-5x+5=0 | B.x2+5x+5="0" | C.x2+5x-5=0 | D.x2+5=0 |
如图是胡老师画的一幅写生画,四位同学对这幅画的作画时间作了猜测. 根据胡老师给出的方向坐标,猜测比较合理的是 ( )
| A.小明:“早上8点” | B.小亮:“中午12点” |
| C.小刚:“下午5点” | D.小红:“什么时间都行” |
甲乙两地相距100km,汽车从甲地开往乙地,所需时间t(小时)和速度v(km/h)之间的函数关系图象大致是下图中( )
若梯形中位线的长是高的2倍,梯形的面积是18cm2,则这个梯形的高等于
| A.6cm | B.6 cm | C.3cm | D.3 cm |
在拼图游戏中,从图1的四张纸片中,任取两张纸片,能拼成“小房子”(如图2)的概率等于 
| A.1 | B. |
C. |
D. |
如图,在△ABC中,AB=AC=BD,AD=CD,则∠ADB的度数是( )
| A.36° | B.45° | C.60° | D.72° |
△ABC中,∠A,∠B均为锐角,且有 ,则△ABC是( )
,则△ABC是( )
| A.直角(不等腰)三角形 | B.等腰直角三角形 |
| C.等腰(不等边)三角形 | D.等边三角形 |
某商品成本价为300元,两次降价后现价为160元,若每次降价的百分率相同,设降价的百分率为x,则方程为__________
为了估计不透明的袋子里装有多少白球,先从袋中摸出10个球都做上标记,然后放回袋中去,充分摇匀后再摸出10个球,发现其中有一个球有标记,那么你估计袋中大约有______个白球
已知:如图梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O,写出图中的全等三角形:___________
如图△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=1,那么PP′有长等于__________
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AB,BD, BC,AC的中点。
(1)求证:四边形EFGH是平行四边形;
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论。
我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是




A B C D
方程x2 = 2x的解是
| A.x=2 | B.x1= ,x2= 0 ,x2= 0 |
C.x1=2,x2=0 | D.x = 0 |
长城总长约为6700010米,用科学记数法表示是(保留两个有效数字)
| A.6.7×105米 | B.6.7×106米 | C.6.7×107米 | D.6.7×108米 |
函数y= (k≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的
(k≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的
A、第一、三象限 B、第三、四象限 C、A、第一、二象限 D、第二、四象限
中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖。参加这个游戏的观众有三次翻牌的机会。某观众前两次翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是
A.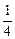 |
B.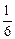 |
C.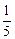 |
D. |
实数a、b在数轴上的位置如图所示,那么化简|a-b|-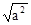 的结果是
的结果是
| A.2a-b | B.b | C.-b | D.-2a+b |
一件衣服标价132元,若以9折降价出售,仍可获利10%,则这件衣服的进价
| A.106元 | B.105元 | C.118元 | D.108元 |
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是
A、 B、
B、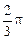 C、
C、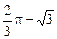 D、
D、
图(1)(2)是根据某地近两年6月上旬日平均气温情况绘制的折线统计图,通过观察图表,可以判断这两年6月上旬气温比较稳定的年份是__。
如图,口ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为8,△FCB的周长为22,则FC的长为_
大楼AD的高为10米,远处有一塔BC,某人在楼底A处测得踏顶B处的仰角为60º,爬到楼顶D点测得塔顶B点的仰角为30º,求塔BC的高度
下图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图

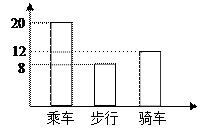
(1)求该班有多少名学生?
(2)补上步行分布直方图的空缺部分;
(3)在扇形统计图中,求骑车人数所占的圆心角度数。
(4)若全年级有500人,估计该年级步行人数
某工程,甲工程队单独做40天完成,若乙工程队单独做30天后,甲、乙两工程队再合作20天完成。
(1)求乙工程队单独做需要多少天完成?
(2)将工程分两部分,甲做其中一部分用了x天,乙做另一部分用了y天,其中x、y均为正整数,且x<15,y<70,求x、y.
已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴相交于点E,点B(-1,0),P是AC上的一个动点(P与点A、C不重合)

(1)求点A、E的坐标;
(2)若y= 过点A、E,求抛物线的解析式。
过点A、E,求抛物线的解析式。
(3)连结PB、PD,设L为△PBD的周长,当L取最小值时,求点P的坐标及L的最小值,并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由
 的值为0,则x的值为
的值为0,则x的值为 



 ,
, ,
, ,……,若
,……,若 (a、b都是正整数),则a+b的最小值是
(a、b都是正整数),则a+b的最小值是 )0+(
)0+( )-1-
)-1- -|-1|
-|-1|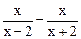 )÷
)÷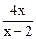 ,其中x=2005
,其中x=2005
 粤公网安备 44130202000953号
粤公网安备 44130202000953号