如图, 已知抛物线 与x轴相交于A、B,点B的坐标为(10,0),顶点M的坐标为(4,8),点P从点M出发,以每秒1个单位的速度沿线段MA向A点运动;点Q从点A出发,以每秒2个单位的速度沿AB向B点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟。
与x轴相交于A、B,点B的坐标为(10,0),顶点M的坐标为(4,8),点P从点M出发,以每秒1个单位的速度沿线段MA向A点运动;点Q从点A出发,以每秒2个单位的速度沿AB向B点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟。
(1)求抛物线的解析式;
(2)设△APQ的面积为S,求S与t之间的函数关系式,△APQ的面积是否有最大值?若有,请求出其最大值;若没有,请说明理由;
(3)当t为何值时,△APQ为等腰三角形?
相关知识点
推荐套卷

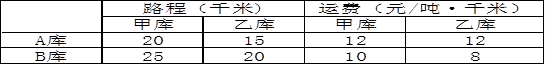
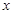 吨,请写出将粮食运往A、B两库的总运费
吨,请写出将粮食运往A、B两库的总运费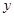 (元)与
(元)与
 粤公网安备 44130202000953号
粤公网安备 44130202000953号