如图所示,在矩形ABCD中,AB=6,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是
如图,已知直角△ACB,AC=1,BC=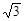 ,过直角顶点C作
,过直角顶点C作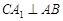 ,垂足为
,垂足为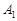 ,再过
,再过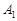 作
作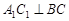 ,垂足为
,垂足为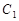 ;过
;过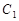 作
作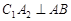 ,垂足为
,垂足为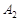 ,再过
,再过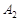 作
作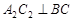 ,垂足为
,垂足为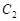 ;……,这样一直做下去,得到一组线段
;……,这样一直做下去,得到一组线段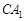 ,
,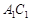 ,
,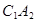 ,……,则第12条线段
,……,则第12条线段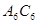 =_______▲ ______.
=_______▲ ______.
如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜, 光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知 AB⊥BD,CD⊥BD,垂足分别为B、D,且测得AB=1.2m,BP=1.8m,PD=12m,那么该古城墙的高度是_____▲______m.
矩形纸片ABCD中,AB=5,AD=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为 ▲ ;
如图(5),已知∠MON=30°,AB⊥ON,垂足为点A,点B在射线OM上,AB=1cm,在射线ON上截取OA1=OB,过A1作A1B1∥AB,A1B1交射线OM于点B1,再在射线ON上截取OA2=OB1,过点A2作A2B2∥AB,A2B2交射线OM于点B2;… 依次进行下去,则A1B1线段的长度为 ,A10B10线段的长度为 .
如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;
取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4的面积为______________. 
如图,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的面积为 ▲ .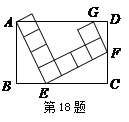
将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=4,AC=6,BC=8,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是___________.
将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF。已知AB=AC=8,BC=10,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.
△ABC中,AB=3cm,BC=4cm,点P沿AB边以1cm/s的速度从点A向点B移动,同时点Q沿BC边以2cm/s的速度从点B向点C移动.若以点P、B、Q构成的三角形与△ABC相似,则运动时间为 秒.
如图,一系列“黑色梯形”是由x轴、直线y= x和过x轴上的正奇数1、3、5、7、9、…所对应的点且与y轴平行的直线围成的.从左到右,将其面积依次记为S1、S2、S3、…、Sn、….则S1= ,Sn= .
x和过x轴上的正奇数1、3、5、7、9、…所对应的点且与y轴平行的直线围成的.从左到右,将其面积依次记为S1、S2、S3、…、Sn、….则S1= ,Sn= .
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是 .
如图,在Rt 中,
中, ,点
,点 在
在 上,且
上,且 ,
, ,若将
,若将 绕点
绕点 顺时针旋转得到Rt
顺时针旋转得到Rt ,且
,且 落在
落在 的延长线上,联结
的延长线上,联结 交
交 的延长线于点
的延长线于点 ,则
,则 = ▲ .
= ▲ . 