初中数学相似多边形的性质填空题

如图，在正方形ABCD中，E为AB中点，G、F分别是AD、BC边上的点，若AG＝1，BF＝2，∠GEF
＝90°，则GF的长为________．

如图，平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，CD=2DE．若△DEF的面积为a，则平行四边形ABCD的面积为　  ▲ 　（用a的代数式表示）．

如图，点P是矩形ABCD的边AD的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是        .

如图，△ABC中，∠ACB=90°，AB=8cm，D是AB的中点．现将△BCD沿BA方向平移1cm，得到△EFG，FG交AC于H，则GH的长等于　 ▲ 　cm．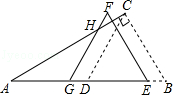

如图，在平行四边形ABCD中，AD=10cm，CD=6cm，E为AD上一点，且BE=BC，CE=CD，则DE=   ▲  cm

已知菱形ABCD的边长是6，点E在直线AD上，DE=3，连接BE，与对角线AC相交于点M，则的值是       

如图,在△ABC中，AB＝AC＝5，BC＝6，点E、F分别在AB、BC边上，将△BEF沿直线EF翻折后，点B落在对边AC的点为B＇，若△B＇FC与△ABC相似，那么BF＝          .

如图，DE是△ABC的中位线，M、N分别是BD、CE的中点，则△ADE与四边形BCNM的面积之比等于           .

如图，以点O为位似中心，将五边形ABCDE放大后得到五边形，已知OA=10cm，=20cm，则五边形ABCDE的周长与五边形的周长的比值是______.

如图：直线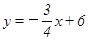与x，y轴分别交于A，B，C是AB的中点，点P从A出发以每秒1个单位的速度沿射线AO方向运动，将点C绕P顺时针旋转90°得到点D，作DE⊥x轴，垂足为E，连接PC，PD，PB.设点P的运动时间为t秒（0≤t≤16）,当以P，D，E为顶点的三角形与△BOP相似时，写出所有t的值：   ▲    ．

如图，在△ABC中，点D在 AB上，请再添加一个适当的条件，使△ADC与△ACB相似，那么要添加的条件是                   ．(只填一个即可)

如图，正方形ABCD的边长为10，内部有6个全等的正方形，小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上，则QB的长为            ．

如图，直角梯形ABCD中，AD∥BC，∠A=∠B=90°，AB=7，AD=2，BC=3，如果在边AB上取一点P使得以P、A、D为顶点的三角形和以P、B、C为顶点的三角形相似，则AP的长为              。

平行四边形ABCD中，点E在边BC上，BE︰EC=1︰2 连结AE交BD于F，则△BFE与△DFA的面积之比为        。

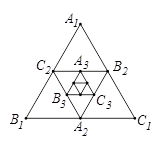
如图，已知正△A₁B₁C₁边长为1，分别取△A₁B₁C₁三边的中点A₂，B₂，C₂，得到△A₂B₂C₂，用同样的方法，得到△A₃B₃C₃，以此下去，正△A_nB_nC_n的面积是        .