初中数学相似多边形的性质填空题

设点P是△ABC内任意一点．现给出如下结论：
①过点P至少存在一条直线将△ABC分成周长相等的两部分；
②过点P至少存在一条直线将△ABC分成面积相等的两部分；
③过点P至多存在一条直线将△ABC分成面积相等的两部分；
④△ABC内存在点Q，过点Q有两条直线将其平分成面积相等的四个部分．
其中结论正确的是　 　．（写出所有正确结论的序号）

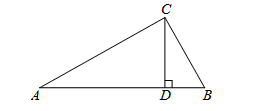
如图，△ABC中，D为BC上一点，∠BAD=∠C，AB=3，BD=2，则CD的长为      ．

梯形ABCD中，AB∥CD，AB=3，CD=8，点E是对角线AC上一点，连接DE并延长交直线AB于点F，若=2，则=　 　．

如图，□ABCD中，E是边BC上一点，加交BD于点F，若BE=2，EC=3，则的值为__________．

如图，已知△ABC是面积为的等边三角形，△ABC∽△ADE，AB＝2AD，∠BAD＝45°，AC与DE相交于点F，则△AEF的面积等于       （结果保留根号）．

如图，AB∥CD∥EF，AC=2，EC=3，BD=3，则BF=          ．

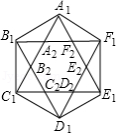
如图，正六边形 $A_1{B}_1{C}_1{D}_1{E}_1{F}_1$的边长为1，它的六条对角线又围成一个正六边形 $A_2{B}_2{C}_2{D}_2{E}_2{F}_2$，如此继续下去，则正六边形 $A_4{B}_4{C}_4{D}_4{E}_4{F}_4$的面积是　　．

如图，一斜坡AB长80m，高BC为5m，将重物从坡底A推到坡上20m的M处停下，则停止地点M的高度为__________

把一个矩形剪去一个正方形，若剩下的矩形与原矩形相似，则原矩形的长边与短边之比为      ．

已知线段，若，且，则_____．

已知AD、BE是锐角△ABC的两条高，且AD、BE交于点H，若，则的值为_________．

如图，直角三角形ABC中，∠ACB=90°，AB=10，BC=6，在线段AB上取一点D，作DF⊥AB交AC于点F，现将△ADF沿DF折叠，使点A落在线段DB上，对应点记为A₁；AD的中点E的对应点记为E₁，若△E₁FA₁∽△E₁BF，则AD=     ．

如图，在△ABC中，CD⊥AB于点D．下列条件：①BC²=BD•BA；②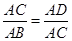；③CD²=AD•BD．其中能证明△ABC是直角三角形的是           ．

已知：△ABC中，点E是AB边的中点，点F在AC边上，若以A，E， F为顶点的三角形与△ABC相似，则需要增加的一个条件是            ．（写出一个即可）

如图,在□ABCD中,点P为边AB上的一点,E,F分别是PD,PC的中点,CD=2．则①EF=      ;②设△PEF,△PAD,△PBC的面积分别为、、．已知,则           ．