下列命题中的真命题是( )
| A.两边和一角分别相等的两个三角形全等 |
| B.相似三角形的面积比等于相似比 |
| C.正方形不是中心对称图形 |
| D.圆内接四边形的对角互补 |
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在运动变化过程中,下列结论:①△DFE是等腰直角三角形;②四边形CEDF不可能为正方形;③四边形CEDF的面积随点E位置的改变而发生变化;④点C、E、D、F四点在同一个圆上,且该圆面积最小为4π;⑤DE•DF+CE•CF的值是定值为8,其中正确结论的个数是( )
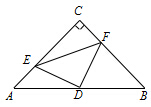
A.4 B.3 C.2 D.1
一块含30°角的直角三角板(如图),它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是( )
| A.5cm | B.6cm | C.(6− )cm )cm |
D.(3+ )cm )cm |
小红利用一些花布的边角料,裁剪后装饰手工画.下面四个图案是她裁剪出的空心等边三角形、菱形、矩形、正方形,若每个图案花边的宽度都相等,那么每个图案中花边的内外边缘所围成的几何图形不一定相似的是( )
A. |
B. |
C. |
D. |
如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分).则下列结论:
①AD=BE=5cm;
②当0<t≤5时, ;
;
③直线NH的解析式为 ;
;
④若△ABE与△QBP相似,则 秒.
秒.
其中正确结论的个数为( )
| A.4 | B.3 | C.2 | D.1 |
如图,等边△ABC的边长为2,DE是它的中位线,则下列三个结论:①DE=1;②△CDE∽△CAB;③△CDE与△CAB的面积之比为1:4.其中正确的有 ( )
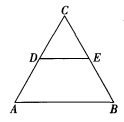
| A.0个 | B.1个 | C.2个 | D.3个 |
如图,矩形 的四个顶点分别在菱形 的四条边上, .将 , 分别沿边 , 折叠,当重叠部分为菱形且面积是菱形 面积的 时,则 为
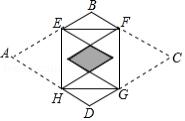
A. B.2C. D.4
如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,则△ABC与△DEF的面积之比为( ).
| A.1:2 | B.1:4 | C.1:5 | D.1:6 |
如图,D、E分别在△ABC的边AB、AC上,要使△AED△与ABC相似,不能添加的条件是( )

A.DE∥BC B.AD•AC=AB•AE
C.AD:AC=AE:AB D.AD:AB=DE:BC
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(2,0),则点C的坐标为( )
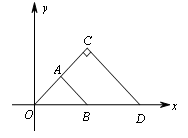
A.(2,2) B.(1,2) C.(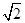 ,2
,2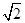 ) D.(2,1)
) D.(2,1)
小明一家人在国庆间自驾汽车从家里出发到某著名旅游景点游玩.他在1:500000的地图上测得家所在的城市与旅游景点所在城市的图上距离为40cm,则这两城市的实际距离为( )
| A.100km | B.200km | C.1000km | D.2000km |
若△ABC∽△A'B'C',∠A=40°,∠C=110°,则∠B'的度数为 ( )
| A.30° | B.50° | C.40° | D.70° |
如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且BD=3AD.那么AE:AC等于( )
A.2 : 3 B.1 : 2 C.1 : 3 D.1 :4