初中数学相似多边形的性质试题

已知△ABC，延长BC到D，使CD=BC．取AB的中点F，连接FD交AC于点E．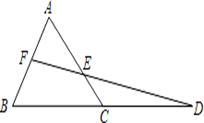

（1）求AE：AC的值；（2）若AB=a，FB=EC，求AC的长．

AD为△ABC的中线，G为△ABC的重心，若=2，则=      ．

如图，梯形ABCD中，AD∥BC，∠ABC=90°，AD=9，BC=12，AB=10，在线段BC上任取一点P，作射线PE⊥PD，与线段AB交于点E，则线段PC的范围是（ ）

A．PC＞0

B．0＜PC＜12

C．3≤PC≤12

D．3＜PC＜12

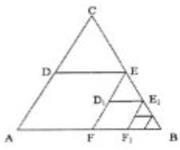
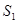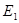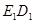如图，△ABC是边长为1的等边三角形，取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作；取BE边中点，作∥FB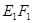，∥EF，得到四边形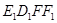，它的面积记作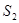．照此规律作下去，则=                ．

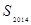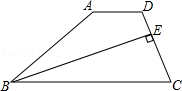
如图，在梯形ABCD中，AD∥BC，BE平分∠ABC交CD于E，且BE⊥CD，CE:ED=2:1．如果△BEC的面积为2，那么四边形ABED的面积是         ．

已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．

（1）如图，已知折痕与边BC交于点E，连结AP、EP、EA．求证：△ECP∽△PDA；
（2）若△ECP与△PDA的面积比为1：4，求边AB的长；
（3）在（2）的条件下以点A为坐标原点，AB所在直线为x轴，AD所在直线为y轴建立平面直角坐标系，问在坐标平面内是否存在点M，使得以点A、B、E、M为顶点的四边形是平行四边形，若存在请直接写出点M的坐标；若不存在请说明理由。

已知Rt△ABC中，AC=BC=2．一直角的顶点P在AB上滑动，直角的两边分别交线段AC，BC于E．F两点

（1）如图1，当=且PE⊥AC时，求证：=；
（2）如图2，当=1时（1）的结论是否仍然成立？为什么？
（3）在（2）的条件下，将直角∠EPF绕点P旋转，设∠BPF=α（0°＜α＜90°）．连结EF，当△CEF的周长等于2+时，请直接写出α的度数．

已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A，C的坐标分别为A（﹣3，0），C（1，0），tan∠BAC=．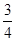

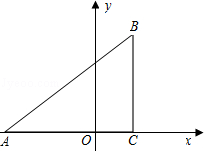
（1）写出点B的坐标；
（2）在x轴上找一点D，连接BD，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；
（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m使得△APQ与△ADB相似？如存在，请求出的m值；如不存在，请说明理由．

（1）如图1，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证：；
（2）如图，△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点．
①如图2，若AB=AC=1，直接写出MN的长；
②如图3，求证：MN²=DM•EN．

将一副三角尺如图所示叠放在一起，则               ．

（本小题满分8分）如图，平面直角坐标系中，将含30°的三角尺的直角顶点C落在第二象限．其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm

（1）若OB=6cm．
①求点C的坐标；
②若点A向右滑动的距离与点B向上滑动的距离相等，求滑动的距离；
（2）点C与点O的距离的最大值．

如图，在平面直角坐标系中，抛物线y=﹣x²+bx+c与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．

（1）求该抛物线的解析式；
（2）当点P在直线BC上方时，请用含m的代数式表示PG的长度；
（3）在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．

（本题14分）如图，在等边中，于点，点在边上运动，过点作与边交于点，连结，以为邻边作□，设□与重叠部分图形的面积为，线段的长为

（1）求线段的长（用含的代数式表示）；
（2）当四边形为菱形时，求的值；
（3）直接写出与之间的函数关系式．

如图，在△ABC中，BA＝BC＝20cm，AC＝30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x秒．

（1）当x为何值时，PQ∥BC；
（2）是否存在某一时刻，使△APQ∽△CQB，若存在，求出此时AP的长；若不存在，请说理由；
（3）当时，求的值．

（1）如图1，两个等边三角形ABC和A₁B₁C₁的中心（点O）相同，且满足AB∥A₁B₁，BC∥B₁C₁，AC∥A₁C₁，可知AB与 A₁B₁，BC与B₁C₁，AC与A₁C₁之间的距离相等，直线MQ分别交三角形相邻两边于点M、N、P、Q，与AB所成夹角为∠α，
①当∠α=30°时，求的值；
②当30°＜∠α＜90°，请用含∠α的式子表示；
（2）如图2，两个正方形ABCD和A₁B₁C₁D₁的中心（点O）相同，且满足AB∥A₁B₁，BC∥B₁C₁，CD∥C₁D₁，AD∥A₁D₁，可知AB与A₁B₁，BC与B₁C₁，CD与C₁D₁，AD与A₁D₁之间的距离相等，直线MQ分别交正方形相邻两边于点M、N、P、Q，与AB所成夹角为∠α，
①当∠α=30°时，求的值；
②当0°＜∠α＜90°，请用含∠α的式子表示；
（3）根据（1）、（2）的研究，如果正n边形（n＞4）的位置关系也满足同样的条件（如图3），正n边形相邻两边被直线MQ截得的两条线段为MN，PQ，请用含m，∠α（0°＜∠α＜90°）的式子表示．