（1）如图1，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证：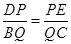
；
（2）如图，△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点．
①如图2，若AB=AC=1，直接写出MN的长；
②如图3，求证：MN2=DM•EN．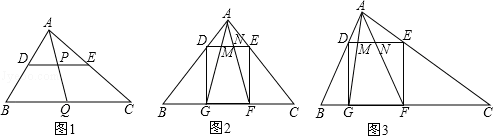
，其中
，
.
；（2）
；（2）
，
，
，
，并比较它们的大小，按从大到小的顺序用“>”连接．
相关知识点
推荐套卷
（1）如图1，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证：；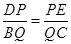
（2）如图，△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点．
①如图2，若AB=AC=1，直接写出MN的长；
②如图3，求证：MN2=DM•EN．
粤公网安备 44130202000953号