(1)问题
如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:AD·BC=AP·BP.
(2)探究
如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用
请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.
如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.
(2)求m与n的函数关系式,直接写出自变量n的取值范围.
(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图12).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD +CE
+CE =DE
=DE .
.
(4)在旋转过程中,(3)中的等量关系BD +CE
+CE =DE
=DE 是否始终成立,若成立,请证明,若不成立,请说明理由.
是否始终成立,若成立,请证明,若不成立,请说明理由.
如图,△ABC是一张直角三角形彩色纸,AC=15cm,BC=20cm.若将斜边上的高CD 分成n等分,然后裁出(n﹣1)张宽度相等的长方形纸条.则这(n﹣1)张纸条的面积和是 cm2.
如图,在平面直角坐标系中,抛物线y=﹣ x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)如图1,当∠ABE=45°,c=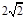 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠ABE=30°,c=4时,a= ,b= ;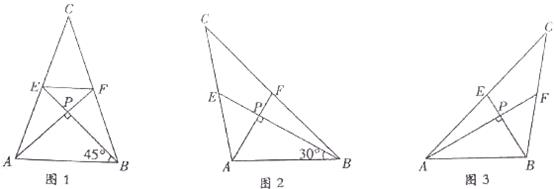
归纳证明
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=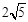 ,AB=3.求AF的长.
,AB=3.求AF的长.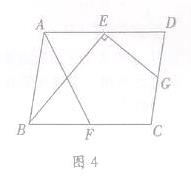
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在□ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值.
的值.
(1)尝试探究
在图1中,过点E作 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 , 的值是
的值是
(2)类比延伸
如图2,在原题的条件下,若 (m>0),则
(m>0),则 的值是 (用含
的值是 (用含 的代数式表示),试写出解答过程.
的代数式表示),试写出解答过程.
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若 ,
, (
( ,
, ),则
),则 的值是 (用含a、b的代数式表示).
的值是 (用含a、b的代数式表示).


如图,在平面直角坐标系
中,直线
与
轴交于点
,与
轴交于点
.抛物线
的对称轴是
且经过
、
两点,与
轴的另一交点为点
.

(1)①直接写出点
的坐标;②求抛物线解析式.
(2)若点
为直线
上方的抛物线上的一点,连接
.求
的面积的最大值,并求出此时点
的坐标.
(3)抛物线上是否存在点
,过点
作
垂直
轴于点
,使得以点
、
、
为顶点的三角形与
相似?若存在,求出点
的坐标;若不存在,请说明理由.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
(1)当x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ∽△CQB,若存在,求出此时AP的长;若不存在,请说理由;
(3)当 时,求
时,求 的值.
的值.
如图1,四边形ABCD中,AD∥BC,∠A=90°,BD⊥CD,AD=
 ,BC=5
,BC=5 ,动点P从点D出发,以1cm/s的速度沿DB方向运动,动点Q也从点D出发,以
,动点P从点D出发,以1cm/s的速度沿DB方向运动,动点Q也从点D出发,以
 /
/ 的速度沿DC方向运动,P,Q两点同时出发,当点Q到达点C时停止运动,点P也随之停止,设运动时间为
的速度沿DC方向运动,P,Q两点同时出发,当点Q到达点C时停止运动,点P也随之停止,设运动时间为
 (
( >0).
>0).
(1)求线段DB的长;
(2)请判断PQ与BC的位置关系,并加以证明;
(3)伴随P,Q两点的运动,将△DPQ绕点P旋转,得到△PMN,点M落在线段PQ上,若△PMN
与△DBC的重叠部分的图形周长为y,
①请求出y与 之间的函数关系式,并指出自变量
之间的函数关系式,并指出自变量 的取值范围;
的取值范围;
②求出当4<y≤5时 的取值范围.
的取值范围.
如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,边AE上有一动点P(不与A,E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.

(1)直接写出 D,E 两点的坐标,D( ),E( )
(2)求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,S有最大值?
(3)当t为何值时,DP平分∠EDA?
(4)当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标.
如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使得两个直角的顶点重合于对角线BD上一点P,EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是正方形ABCD的中心;
②当x= 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ;
;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确的是________(填序号).
有两个直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=4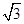 ,将这两个直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
,将这两个直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC= 度;
(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围(直接写出结果,不必写过程).
如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
①当 时,
时, ;
;
②当 时,
时,
(2)拓展探究
试判断:当0°≤α<360°时,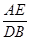 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.

已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连接FD交AC于点E.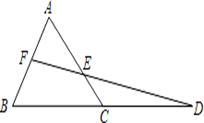
(1)求AE:AC的值;(2)若AB=a,FB=EC,求AC的长.