初中数学相似多边形的性质试题

已知：如图，在ΔABC中，AB=AC=10cm，BC=12cm，AD⊥BC于D．直线PM从点C出发沿CB方向匀速运动，速度为1 cm/s；运动过程中始终保持PM⊥BC，直线PM交BC于P，交AC于M ；过点P作PQ⊥AB，交AB于Q，交AD于N ，连接QM．设运动时间是t（s）（0＜t ＜6），解答下列问题：

（1）当t为何值时，QM∥BC?
（2）设四边形ANPM的面积为y（cm²），试求出y与t的函数关系式；
（3）是否存在某一时刻t，使y的值最大？若存在，求出t的值；若不存在，请说明理由；
（4）是否存在某一时刻t，使点M在线段PQ的垂直平分线上？若存在，求出t的值；若不存在，请说明理由．

如图1，在四边形ABCD中，点E、F分别是AB、CD的中点，过点E作AB的垂线，过点F作CD的垂线，两垂线交于点G，连接AG、BG、CG、DG，且∠AGD＝∠BGC．
（1）求证：AD＝BC；
（2）求证：△AGD∽△EGF；
（3）如图2，若AD、BC所在直线互相垂直，求的值．

如图，矩形ABOD的两边OB，OD都在坐标轴的正半轴上，OD=3，另两边与反比例函数的图象分别相交于点E，F，且DE=2．过点E作EH⊥x轴于点H，过点F作FG⊥EH于点G．回答下面的问题：
（1）该反比例函数的解析式是什么？
（2）当四边形AEGF为正方形时，点F的坐标时多少？
（3）阅读合作学习内容，请解答其中的问题；
小亮进一步研究四边形AEGF的特征后提出问题：“当AE＞EG时，矩形AEGF与矩形DOHE能否全等？能否相似？”
针对小亮提出的问题，请你判断这两个矩形能否全等？直接写出结论即可；这两个矩形能否相似？若能相似，求出相似比；若不能相似，试说明理由．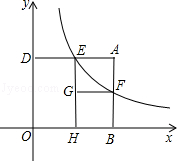

如图，Rt△ABC中，∠ACB=Rt∠,AC=2BC=2,作内接正方形A₁B₁D₁C；在Rt△AA₁B₁中，作内接正方形A₂B₂D₂A₁；在Rt△AA₂B₂中，作内接正方形A₃B₃D₃A₂；……；依次作下去，则第n个正方形A_nB_nD_nA_n-1的边长是（     ）

A．

B．

C．

D．

已知直角坐标系中菱形ABCD的位置如图所示，C．D两点的坐标分别为 （4，0）、（0，3）．现有两动点P、Q分别从A、C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为ts．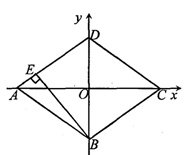

（1）菱形ABCD的边长是   ，面积是   ， 高BE的长是   ．（直接填写结果）
（2）探究下列问题：
①若点P的速度为1cm/s，点Q的速度为2 cm/s．当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式，以及S的最大值；
②若点P的速度为1cm/s，点Q的速度变为kcm/s，在运动过程中，任何时刻都有相应的k值，使得△APQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形，请探究当t＝4s时的情形，并求出k的值．

如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数的图象上，从左向右第3个正方形中的一个顶点A的坐标为（27，9），阴影三角形部分的面积从左向右依次记为S₁、S₂、S₃、…、S_n，则第4个正方形的边长是    , S₃的值为  ．

如图1，△ABC中，AB=AC，点D在BA的延长线上，点E在BC上，DE=DC，点F是DE与AC的交点，且DF=FE．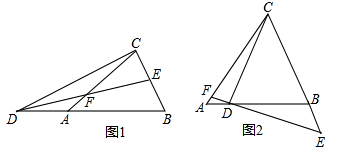

（1）图1中是否存在与∠BDE相等的角？若存在，请找出，并加以证明，若不存在，说明理由；
（2）求证：BE=EC；
（3）若将“点D在BA的延长线上，点E在BC上”和“点F是DE与AC的交点，且DF=FE”分别改为“点D在AB上，点E在CB的延长线上”和“点F是ED的延长线与AC的交点，且DF=kFE”，其他条件不变（如图2）．当AB=1，∠ABC=a时，求BE的长（用含k、a的式子表示）．

如图，在△中，∠90°，，，点从点出发，沿以
2㎝的速度向点移动，点从点出发，以的速度向点移动，若点分别从点同时出发，
设运动时间为，当为何值时，△与△相似？

如图①，直线l：y=mx+n（m＜0，n＞0）与x，y轴分别相交于A，B 两点，将△AOB绕点O逆时针旋转90°，得到△COD，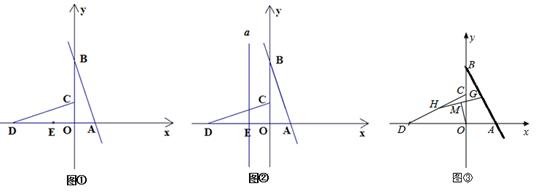

（1）若l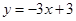：，E为AD的中点
①在CD上有一动点F ，求当△DEF与△COD相似时点F的坐标；
②如图②，过E作x轴的垂线a，在直线a上是否存在一点Q，使∠CQO=∠CDO？若存在，求出Q点坐标；若不存在，请说明理由
（2）如图③，若l：y=mx﹣4m，G为AB中点，H为CD中点，连接GH，M为GH中点，连接OM．若OM=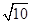，直接写出l的函数解析式．

△OAB的坐标分别为O（0，0），A（0，4），B（3，0），以原点为位似中心，在第一象限将△OAB扩大，使变换得到的△OEF与△OAB对应边的比为2∶1，

（1）画出△OEF；
（2）求四边形ABFE的面积．

如图，已知正方形ABCD，点E是边AB上一点，点O是线段AE上的一个动点（不与A、E重合），以O为圆心，OB为半径的圆与边AD相交于点M，过点M作⊙O的切线交DC于点N，连结OM、ON、BM、BN．

求证：（1）△AOM∽△DMN； （2）求∠MBN的度数．

如图，在Rt△ABC中，∠C=90°．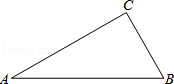

（1）根据要求用尺规作图：过点C作斜边AB边上的高CD，垂足为D（不写作法，只保留作图痕迹）；
（2）在（1）的条件下，请写出图中所有与△ABC相似的三角形．

如图（a），在平面直角坐标系中，点A坐标为（12，0），点B坐标为（6，8），点C为OB的中点，点D从点O出发，沿△OAB的三边按逆时针方向以2个单位长度/秒的速度运动一周．
（1）点C的坐标是       ，当点D运动8.5秒时所在位置的坐标是        ；
（2）设点D运动的时间为t秒，试用含t的代数式表示△OCD的面积S，并指出t为何值时，S最大；
（3）如图（b），另有一点E在线段AB上以同样速度由点A向点B运动，若点E与点D同时出发，问在运动5秒钟内，以点D、A、E为顶点的三角形何时与△OCD相似？（只考虑以点A、O为对应顶点的情况）

如图1，在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，点D是BC上一定点．动点P从C出发，以2cm/s的速度沿C→A→B方向运动，动点Q从D出发，以1cm/s的速度沿D→B方向运动．点P出发5 s后，点Q才开始出发，且当一个点达到B时，另一个点随之停止．图2是当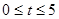时△BPQ的面积S（cm²）与点P的运动时间t（s）的函数图象．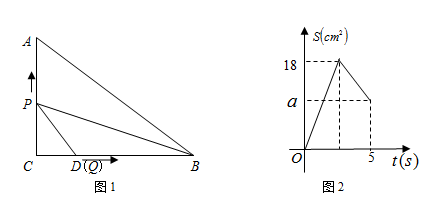

（1）CD =        ，        ；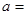
（2）当点P在边AB上时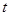，为何值时，使得△BPQ与△ABC为相似？
（3）运动过程中，求出当△BPQ是以BP为腰的等腰三角形时的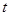值．

已知：如图，矩形ABCD中，CD＝2，AD＝3，以C点为圆心，作一个动圆，与线段AD交于点P（P和A、D不重合），过P作⊙C的切线交线段AB于F点．

（1）求证：△CDP∽△PAF；
（2）设DP＝x，AF＝y，求y关于x的函数关系式，及自变量x的取值范围；
（3）是否存在这样的点P，使△APF沿PF翻折后，点A落在BC上，请说明理由．