兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.5米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为( )
| A.9.5米 | B.10.75米 | C.11.8米 | D.9.8米 |
下列各组线段中,成比例线段的是( )
| A.4cm、2cm、1cm、3cm | B.1cm、2cm、3cm、5cm |
| C.3cm、4cm、5cm、6cm | D.1cm、2cm、2cm、4cm |
如图,在矩形ABCD中,AB=9,AD=12.动点E从点B出发,沿线段BC(不包括端点B、C)以每秒2个单位长度的速度,匀速向点C运动;动点F从点C出发,沿线段CD(不包括端点C、D)以每秒1个单位长度的速度,匀速向点D运动;点E、F同时出发,同时停止.连接AF并延长交BC的延长线于点M,再把AM沿AD翻折交CD延长线于点N,连接MN.设运动时间为t秒.
(1)当t为何值时,△ABE∽△ECF;
(2)在点E运动的过程中是否存在某个时刻使AE⊥AN?若存在请求出t的值,若不存在请说明理由;
(3)在运动的过程中,△AMN的面积是否变化?如果改变,求出变化的范围;如果不变,求出它的值.
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点, .已知关于x,y的二元一次方程
.已知关于x,y的二元一次方程 (m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )
(m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )
A. |
B.1 | C. |
D. |
如图,在 中,
中, ,那么下列等式中,成立的是( )
,那么下列等式中,成立的是( )

A. |
B. |
C. |
D. |
(满分14分)如图,已知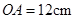 ,
,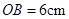 ,点
,点 从点
从点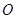 开始沿
开始沿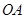 边向点
边向点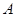 以
以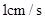 的速度移动,点
的速度移动,点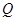 从点
从点 开始向点
开始向点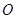 以相同的速度移动,若
以相同的速度移动,若 、
、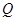 同时出发,移动时间为
同时出发,移动时间为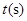 (0≤
(0≤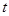 ≤6).
≤6).
(1)设 的面积为
的面积为 ,求
,求 关于
关于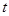 的函数解析式;
的函数解析式;
(2)当 的面积最大时,
的面积最大时, 沿直线
沿直线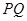 翻折后得到
翻折后得到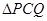 ,试判断点
,试判断点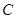 是否落在直线
是否落在直线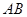 上,并说明理由.
上,并说明理由.
(3)当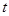 为何值时,
为何值时, 与
与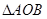 相似.
相似.
如图,在阳光下某一时刻大树AB的影子落在墙DE上的C点,同时1.2 m的标杆影长3 m,已知CD=4m,BD="6" m,求大树的高度.
下列条件能判断△ABC与△DEF相似的有( )
(1)∠A=∠D,∠E=∠C;
(2) ;
;
(3)
(4) ;
;
(5)∠A=∠D,
| A.2个 | B.3个 | C.4个 | D.5个 |
如图:为了测量某棵树的高度,小刚用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离6m,与树相距15m,那么这棵的高度为( )
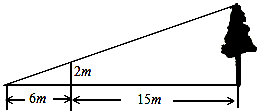
| A.5米 | B.7米 | C.7.5米 | D.21米 |
如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是 ( )

A. B.
B. C.
C. D.
D.
下列说法中正确的是( )
| A.两个直角三角形相似 | B.两个等腰三角形相似 |
| C.两个等边三角形相似 | D.两个锐角三角形相似 |