如图,在△ABC中,DE∥BC,分别交AB,AC于点D、E.若AD=3,DB=2,BC=6,则DE的长为 .

如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC= 时,图中的两个三角形相似.(只需写出一个条件即可)

如果两个相似三角形对应高之比是9∶16,那么它们的对应周长之比是 ( )
| A.3∶4 | B.4∶3 | C.9∶16 | D.16∶9 |
若5a=3b(a、b均不为0)那么b:a=( ):( ).
如图在4×4的方格纸(每小方格的面积为1)上有一个格点三角形ABC(图甲),请在图乙、图丙、图丁中画出与三角形ABC相似(不全等)的格点三角形.
如图,铁路道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高(杆的宽度忽略不计)
| A.12m | B.8m | C.6m | D.4m |
如图,在△ABC中,DE∥BC, ,△ADE的面积为8,则四边形DBCE的面积为( )
,△ADE的面积为8,则四边形DBCE的面积为( )

| A.10 | B.4 | C.42 | D.18 |
如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,则△ABC与△DEF的面积之比为( )

| A.1:2 | B.1:4 | C.1:5 | D.1:6 |
下列条件能判断△ABC与△DEF相似的有( )
(1)∠A=∠D,∠E=∠C;
(2) ;
;
(3)
(4) ;
;
(5)∠A=∠D,
| A.2个 | B.3个 | C.4个 | D.5个 |
如图:为了测量某棵树的高度,小刚用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离6m,与树相距15m,那么这棵的高度为( )
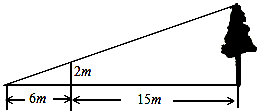
| A.5米 | B.7米 | C.7.5米 | D.21米 |
如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是 ( )

A. B.
B. C.
C. D.
D.
下列说法中正确的是( )
| A.两个直角三角形相似 | B.两个等腰三角形相似 |
| C.两个等边三角形相似 | D.两个锐角三角形相似 |